マクマネー検定

対応ありの分割表と、対応なしの分割表のうち、対応ありの分割表に使う検定が、マクマネー検定です。ノンパラメトリック検定の一種として、紹介されることが多いです。

独立性の検定は、対応なしの分割表に使います。関係がない場合、表の中の値は、ほぼ均等になるはずです。独立性の検定では、何らかの関係があると、値が偏って来ると考えます。

マクマネー検定の仕組み

クロス集計
上のような分割表に対して、マクマネー検定では、(b - c)と、(b + c)だけから、以下の量を作って、これをカイ二乗検定をします。
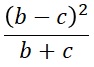
McNemer

aとdは、AとBという２種類の評価に対して、（合格-合格）や（不合格-不合格）のように、いずれも同じになるような度数が入るようにします。

bとcは、（合格-不合格）や（不合格-合格）のように、評価が変わったもの、ということになります。

マクマネー検定が見るのは、bとcの差です。これによって、評価に違いがあるのかを見ます。

マクマネー検定は、bとcの違いしか見ないので、aとdは無関係になっています。

aとdは無関係なので、データ全体の量に対して、bとcの差がどのようなものなのかは評価していないです。

データ全体に対して評価するのなら、分母は、b+cではなく、a+b+c+dの方が良さそうです。

マクマネー検定と独立性の検定は、「対応のある・なし」という違いで説明されることが一般的のようです。

「対応のある・なし」という事と、検定している内容との関連が議論されることは、あまりないようですが、議論するなら、以下の違いがあります。

「医療統計学　基礎統計から多変量解析まで」　松木秀明・須藤真由美・松木勇樹　著　東海大学出版部　2014
マクマネー検定は、対応のある場合の独立性の検定として、SPSSでの例も使って、解説しています。