検定 は、「違いがあると言えるのか？」という事について、定量的な分析ができます。
平均値の差の検定 は、検定の中でも基本的なものになります。 データは、２列あって、１列目と２列目を比べることを想定しています。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
t.test(x=Data$X1,y=Data$X2,var.equal=T,paired=F) # スチューデントのt検定
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
t.test(x=Data$X1,y=Data$X2,var.equal=F,paired=F) # ウェルチのt検定
library("exactRankTests")
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
wilcox.exact(x=Data$X1,y=Data$X2,paired=F) # ウィルコクソンの順位和検定
２つ以上の母平均の差の検定は、「 分散分析 」と呼ばれているものがあります。
データは、１列目は「X」という列名でカテゴリ、２列目は「Y」という列名で数値が入っていることを想定しています。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
summary(aov(Y~X,data=Data)) # 一元配置分散分析
データは、１列目、２列目は「X1」、「X2」という列名で水準名、３列目は「Y」という列名で数値が入っていることを想定しています。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
summary(aov(Y~X1+X2,data=Data)) # 二元配置分散分析（交互作用項なし）
交互作用 も評価する場合は、「+」の所が、「*」になります。
交互作用項を入れる場合は、繰り返しデータが必要になります。 繰り返しデータとは、２つの因子のそれぞれの水準の組み合わせについて、複数回分のデータがあることを指します。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
summary(aov(Y~X1*X2,data=Data)) # 二元配置分散分析（交互作用項あり）
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
kruskal.test(x=list(Data$X1,Data$X2))# クラスカル-ウォリス検定
対応のありの平均値の差の検定 です。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
t.test(x=Data$X1,y=Data$X2,paired=T) # 対応のある平均値の差の検定
library("exactRankTests")
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
wilcox.exact(x=Data$X1,y=Data$X2,paired=T) # ウィルコクソンの順位和検定
library(DescTools)
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
SignTest(x=Data$X1,y=Data$X2) # 符号検定
データは、１列目、２列目は「X1」、「X2」という列名でカテゴリ、３列目は「Y」という列名で数値が入っていることを想定しています。 「X2」が対応を表す文字列になります。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
summary(aov(Y~X1+X2,data=Data)) # 対応のある一元配置分散分析
ばらつきの違いの検定 です。
データは、２列あって、「X1」、「X2」という列名が１行目にあって、その下に数値が入っていることを想定しています。）
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
var.test(x=Data$X1,y=Data$X2) # ２つの母分散の比の検定
データは、１列目は「X」という列名でカテゴリ、２列目は「Y」という列名で数値が入っていることを想定しています。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
bartlett.test(formula=Data$Y~Data$X) # バートレット検定
Rでできるムッド検定を、素直に検索すると、「stats」というパッケージにある「mood.test」を紹介している記事ばかり出て来るのですが、 「stats」は、CRANの中にないようでした。 代わりのものを探したところ、「coin」の中に、「mood_test」というものがあり、これで代用できました。
coinには、mood_testの他に、taha_test、klotz_test、ansari_testというものもあり、これらもムッド検定と同様に、ばらつきの違いの検定として分類されています。
library("coin")
library(tidyr)
setwd("C:/Rtest")
Data <- read.csv("Data.csv", header=T)
Data_long <- tidyr::gather(Data, key="Xs", value = Val) # ２列のデータを、１列にまとめる
Data_long$Xs <-as.factor(Data_long$Xs)
mood_test(Val ~ Xs, data = Data_long)# ムッド検定
「1/10」と「4/20」の差の検定の場合
prop.test(c(1,4),c(10,20))# 比率の差の検定
カイ二乗検定を使った 独立性の検定 です。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
chisq.test(Data)# カイ二乗検定
マクマネー検定 です。
a b
c d
の行列の場合、下記は、
c(a, c, b, d）とすると同じになります。
mcnemar.test(matrix(c(1, 4, 10, 20), 2, 2)) # マクマネー検定
setwd("C:/Rtest")
Data <- read.csv("Data.csv", header=T)
ks.test(x=Data[,1],y=Data[,2]) # コルモゴロフ-スミルノフ検定
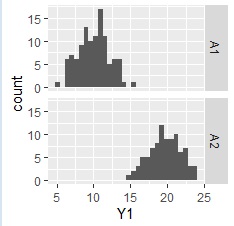
データは、「C1」という列名でカテゴリ、「Y1」という列名で数値が入っていることを想定しています。
ggplot(Data, aes(x=Y1)) + geom_histogram() + facet_grid(C1~.)# 層別ヒストグラムを描く
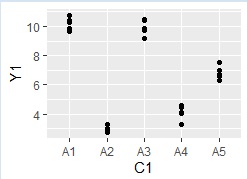
ggplot(Data, aes(x=C1, y=Y1)) + geom_point() # 一次元散布図を描く
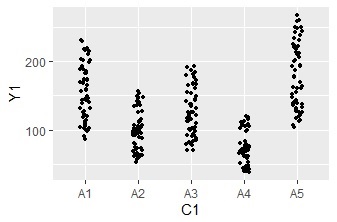
プロットの大きさはsize、横方向の散らばり具合はposition=position_jitterの数字で調節できます。
ggplot(Data, aes(x=C1, y=Y1)) + geom_jitter(size=1, position=position_jitter(0.1))# 一次元ジター散布図を描く
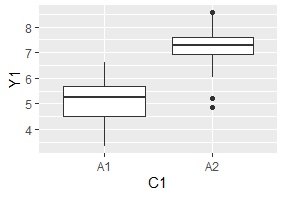
ggplot(Data, aes(x=C1, y=Y1)) + geom_boxplot() # 箱ひげ図を描く
ggplot(Data, aes(x=Y1)) + geom_histogram() + facet_grid(C1+C2~.)# ２段層別ヒストグラムを描く
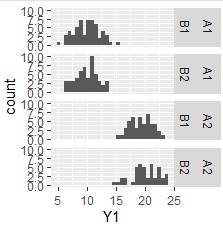
ggplot(Data, aes(x=C1, y=Y1)) + geom_jitter(size=1, position=position_jitter(0.1)) +facet_grid(.~C2)# 一次元散布図（二元配置）を描く
「Package ‘coin’」 2023
coinのマニュアルです。
https://cran.r-project.org/web/packages/coin/coin.pdf
