対応ありの分割表と、対応なしの分割表

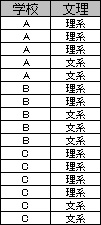
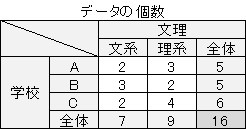
クロス集計
上のデータは、左が２変数の表データで、右がそれを集計した分割表です。見た目が違いますが、両者は、ほぼ同じ内容です。

分割表には、「対応あり」と「対応なし」と呼ばれているものがあります。

量的変数の検定には、対応のある検定と、「対応なしの検定」があります。量的変数の時の、「対応あり・なし」と、分割表の時の、「対応あり・なし」というのは、似ている点と、違う点があります。

似ている点：対応ありの分割表

上記では、学校と文理について、一人ずつのデータがあり、それを集計して分割表を作っています。

「学校を選ぶ事と、文理を選ぶ事は、別の考え方で決まる」とするのなら、統計学的には、「独立している」と呼びます。

量的変数で「対応あり」という場合は、「同じサンプルについての、『前』と『後』のデータ」、「同じサンプルについて、異なる温度計で測ったデータ」といったものがありますが、質的変数でも同様の考え方をします。このような場合は、独立していないです。

このような質的変数を使って作られた分割表が、対応ありの分割表です。

「同じサンプルが２変数の値を持つ」と「２変数は独立していないと考えられる」という、２つの条件がそろうと、「対応あり」となる点は、対応ありの検定でも、分割表でも同じです。

話を最初に戻すと、学校と文理のデータから作ったデータは、対応なしの分割表です。

対応なしの分割表は、「同じサンプルが２変数の値を持つ」と「２変数は独立していると考えられる」という、２つの条件がそろう必要があります。

一方、対応なしの検定は、「２変数は独立していると考えられる」という条件だけです。対応なしの検定は、対応ありの検定と違って、２変数のサンプル数が違っていてもできます。

分割表に対して使う検定は、独立性の検定が有名です

「分割表」と、ひとくくりにされがちですが、独立性の検定は、本来、対応なしの分割表に対して使うものです。

対応ありの分割表に対して、「２変数に違いがあると言えるか？」ということを調べる検定は、マクマネー検定があります。