比例分散
では、
Y = (a + E) * X
という式を扱います。
これが成り立っていて、YとXを逆にしたものは成り立っていない時は、
Y <-- X
というように矢印で表現するようにします。
有向比例分散分析というのは、２つ以上の変数があって、比例分散の関係がある時に、それらの変数が、上記の式のYとXの、どちらに当てはまるのかを調べる方法です。
結果を矢印で表せるので、
有向グラフになるデータの構造
の一種です。
なお、「有向比例分散分析」という名前は、筆者がつけたものです。 比例分散モデルの構造の特定に、歪度や尖度を使うという下記の話は、筆者のアイディアです。 世の中には、先行研究があるかもしれないです。そのような文献をご存知の方は、ご教示いただけると幸いです。
Eが正規分布や一様分布の場合、Eは左右対称の分布になります。 1/Eは、非対称になります。 非対称であればあるほど、歪度（わいど：skewness）の絶対値が大きくなります。この性質を利用します。
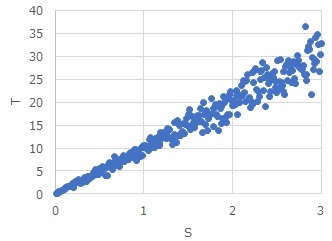
具体的には、２つの変数SとTがあった時に、S/TとT/Sを計算して、それぞれで歪度を計算します。
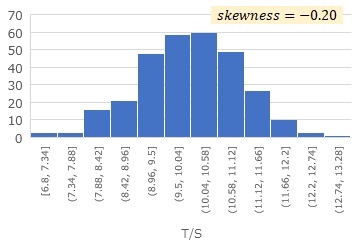
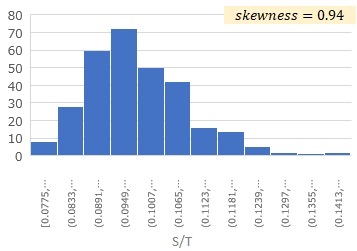
例えば、T/Sの歪度が-0.20で、S/Tの歪度が0.94の場合は、
T = (a + E) * S
というように推定ができます。
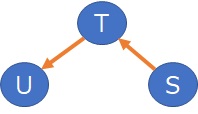
構造を矢印で表すと下のようになります。
T = (a1 + E1) * S
U = (a2 + E2) * T
という関係になっている３変数があったとします。
２変数の時の方法で、歪度を計算すると下のグラフのようになります。
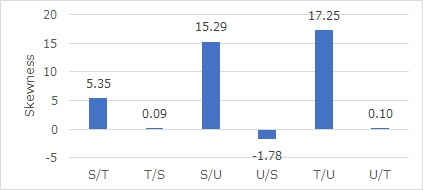
SとT、SとU、TとUについて、それぞれで矢印の向きがわかり、それをそのまま矢印で表現すると下になります。
歪度だけで判断すると、こうなります。
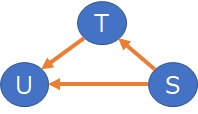
ここでは、SとUの間にも、矢印があります。 元のデータは、SからT、TからUが作られるので、SとUの間の矢印を除去する方法があると良いのですが、なさそうです。 尖度を使うことも考えてみましたが、上記の例で、a1やa2が０の特殊な場合にしか使えない方法でした。 a1やa2が０だと、U/Sの尖度が高くなる特徴があるので、それを使って判定する方法です。
「Eが左右対称の分布」という前提があります。 Xが大きければ大きいほどY方向のばらつきが大きいデータだとしても、Eが左右対称の分布ではない場合はできません。
そのため、Eと1/Eの両方について、ヒストグラムを作って確認した方が良いです。
回帰モデルになるデータの構造 、つまり、Y = X + Eの場合は、Y/Xが非対称になるため、歪度で判断できません。
実際のデータでは、 回帰モデルになるデータの構造 と比例分散モデルのデータ構造は、見分けがつきにくいことがあります。
３変数の場合で、上記の方法で調べられるのは、
のような時です。
１つの変数に、２つの変数が影響している場合、つまり、下のような時は調べられません。
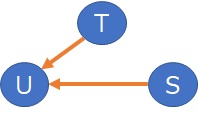
Rによる有向比例分散分析 のページがあります。
順路
次は
誤差の乗法モデル
