計算統計学は、 コンピュータシミュレーション と統計学を組み合わせた分野です。
高度な方法もありますが、「ばらついたデータを作って、数式を検証する」といった計算統計学の入門的な方法だけでも、 現実の問題の解明に役立つことがあります。 筆者自身にもいくつが経験があります。
「計算統計学の入門的な方法だけでも、現実の問題の解明に役立つ」というのは、あまり認知されていませんが、
データサイエンス
の有望な分野です。
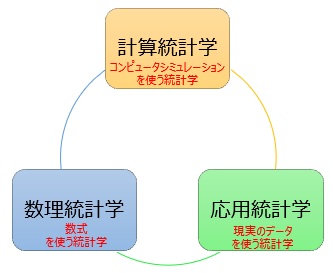
以下は、計算統計学の入門的な方法の使い道です。
統計学の式には、誤差項が入っていることが多いです。これが入っていることで、ばらつきを扱えるようになっています。
ばらつくデータの作り方 を使うと ばらつきモデル の例のようなデータが作れ、「現実に近いか？」、「現実のモデルとして使えそうか？」という調査ができます。
現実に起きるデータのばらつきは、「たまたま」その時に現れたものです。１回分の事しかわかりません。
「たまたまその時は、ひどい事になったのか？」、あるいは、「良く起きることなのか？」という事の調査ができます。 ランダムウォークモデル のページは、その例です。
また、分散の平均値が不偏分散になることは、有名な話ですが、「中央値は？」、「サンプル数が少ない時は、どのくらいばらつく？」といったことは、 理論的なアプローチでは扱いにくいです。 不偏分散 のページでは、計算統計学の視点で不偏分散の特徴を調べています。
現実のデータには、固有の情報や背景が入るので、現実の調査には不可欠です。
一方、 統計学の理論の研究や、理論の勉強の時は、現実のデータが持っている情報がノイズとなってしまい、肝心なところが見えなくなってしまうことがあります。
「一様分布になっているデータ」や、「正規分布で、平均値と標準偏差がわかっているデータ」というものを使うと、 ノイズのない研究や勉強ができるようになります。 また、現実のデータを扱う時に、理論から推定できる部分と、現実のデータならではの部分の切り分けがしやすくなります。
計算統計学と似た分野として、計算物理学があります。
伝統的な物理学は、理論物理学と実験物理学に分かれます。 物理学では、高度な数学が使われることもあり、数学の部分がどうなっているのかを研究するのが理論物理学です。 理論物理学の研究者は、紙とペンだけで研究するスタイルになります。 一方で、実験を通して、物理現象を解明していくのが実験物理学です。
筆者の出身校では、理論物理学と実験物理学の研究室が半々でした。
計算物理学は、ちょうど筆者が大学生だった1990年代に「第３の物理学」として急速に発展した分野です。 実際の「物」を扱わない点は理論物理学と同じなのですが、コンピュータの中で実験（シミュレーション）をするので実験物理学の側面も持っています。
筆者が修士課程の時は、その辺りに魅力を感じて、環境問題への意識も重ねて、 圧電素子の鉛フリー化と、第一原理計算 の研究に進みました。
筆者による上記の説明は、統計学の入門書にあるような内容を、計算統計学を通して理解したり、応用する話です。 筆者が探した時点では、「計算統計学」をタイトルにしている本でそのような内容のものはなく、 数理統計学と組み合わせた高度な話が紹介されています。
「生物学のための計算統計学 最尤法，ブートストラップ，無作為化法」 Derek A.Roff 著 共立出版 2011
最尤法、ジャックナイフ法、ブートストラップ法、無作為化法、各種平滑化法、樹木モデル、ベイズ法を、生物学に応用しています。
従来からあった研究の問題として、自分のデータに対して、選んだ統計手法が妥当かどうかがわからない、というものがあったとしています。
計算統計学は、統計手法の仮定にデータを合わせるのではなく、データの特性に合わせた柔軟な解析ができるもの、としています。
「21世紀の統計科学 Ⅲ 数理・計算の統計科学」 北川源四郎・竹村彰通 編 東京大学出版会 2008
数理統計学と計算統計学の新しい話題を紹介しています。
計算統計学としては、ブートストラップ法、EMアルゴリズム、マルコフ連鎖モンテカルロ法、逐次モンテカルロ法とパーティクルフィルタで、章立てがされています。
「計算統計学の方法」 小西貞則・越智義道・大森裕浩 著 朝倉書店 2008
ブートストラップ法、EMアルゴリズム、マルコフ連鎖モンテカルロ法の３部構成になっています。
「ベイズ計算統計学」 古澄英男 著 朝倉書店 2015
マルコフ連鎖モンテカルロ法の専門書になっています。
ベイズ統計学、モンテカルロ法の章で準備して、マルコフ連鎖モンテカルロ法の章に続きます。
「計算統計 I 確率計算の新しい手法」 汪金芳 他 著 岩波書店 2018
ブートストラップ法、超一様分布列、平均場近似、一般化EM法、変分ベイズ法の解説書です。
「計算統計 Ⅱ マルコフ連鎖モンテカルロ法とその周辺」 伊庭幸人 他 著 岩波書店 2018
マルコフ連鎖モンテカルロ法と逐次モンテカルロ法の解説書です。
「計算統計入門／代数生物学 大規模・高精度計算が拓いた新技法」 手塚集 吉田寛 著 講談社サイエンティフィク 2008
計算統計学と代数生物学は、別の分野ですが、計算機科学の発展に貢献したチューリングの晩年の研究が代数生物学であったので、この本では一冊の中に入れています。
計算統計としては、ビュッフォンの麺、次元の呪い、独立な高次元サンプリング、マルコフ従属なサンプリング、大域感度分析を解説しています。
次は
尤度モデル
