コルモゴロフ-スミルノフ検定 では、上の表のような計算を進めて、経験分布の差分の最大値に着目して行きます。
コルモゴロフ-スミルノフ検定 は、「分布全体の違いを調べる方法」というようにして説明されることが多いようですが、実際は、一番違う部分だけを調べる方法になっています。
そこで、分布全体の違いを方法として、筆者が考案したのが、このページの方法になります。 世の中に、既に同じものがあれば、説明はそれに合わせるつもりですが、さしあたって、なさそうです。
対応のない２標本の類似度分析は、途中までが、 コルモゴロフ-スミルノフ検定 と同じです。
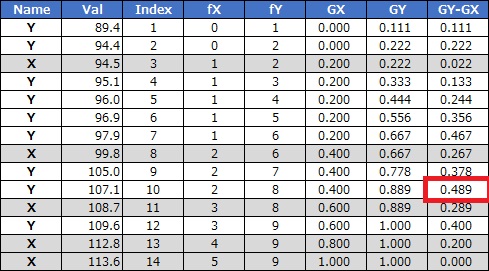
コルモゴロフ-スミルノフ検定
では、上の表のような計算を進めて、経験分布の差分の最大値に着目して行きます。
対応のない２標本の類似度分析は、最大値に着目するのではなく、経験分布の比較や、経験分布の差分全体について、分析を進めます。
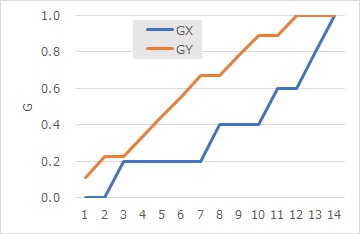
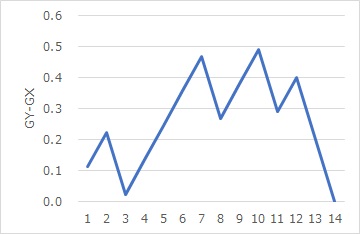
対応のない２標本の類似度分析をした場合に、どのような結果になるのかを、典型的な例で調べたのが下記になります。
サンプル数は10000です。
平均値が０、標準偏差が１の正規分布になるようにして作った２群あります。
厳密には、平均値は、0.002違います。
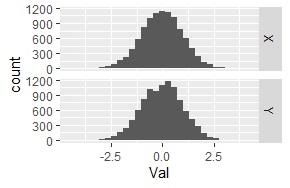
下記は、コルモゴロフ-スミルノフ検定の結果です。
p値が0.305です。
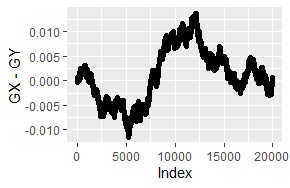
経験分布の差分が、下図になります。
折れ線グラフは、ランダムウォークモデルのような感じです。
ヒストグラムは、プラス側もマイナス側にも広がっています。
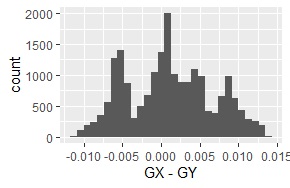
サンプル数は10000です。
両方とも正規分布で、片方は、平均値が０、標準偏差が１、もう片方は平均値が１、標準偏差が１です。
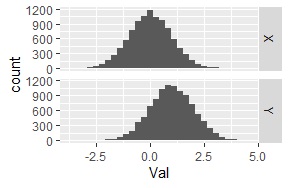
下記は、コルモゴロフ-スミルノフ検定の結果です。
p値は非常に小さいです。
経験分布の差分が、下図になります。
折れ線グラフは、きれいな曲線です。
ヒストグラムは、きれいに偏っています。
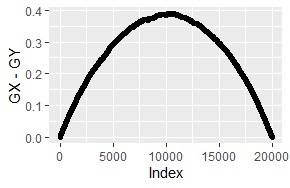
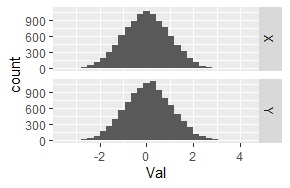
サンプル数は10000です。
両方とも正規分布で、片方は、平均値が０、標準偏差が１、もう片方は平均値0.1、標準偏差が１です。
下記は、コルモゴロフ-スミルノフ検定の結果です。
p値が非常に小さいです。
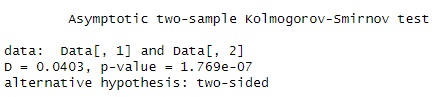
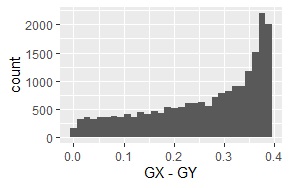
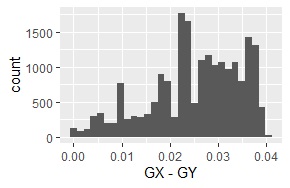
経験分布の差分が、下図になります。
平均値のずれが0.002の時と、１の時の間のようなグラフになっています。
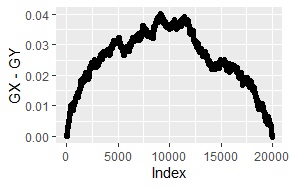
サンプル数は10000です。
平均値は同じです、
片方は、標準偏差が１、もう片方は、標準偏差が５です。
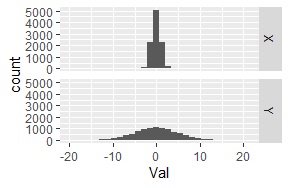
下記は、コルモゴロフ-スミルノフ検定の結果です。
p値が非常に小さいです。
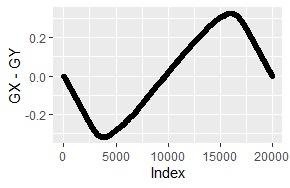
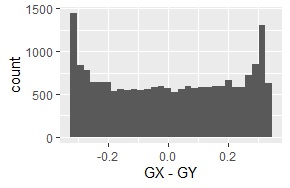
経験分布の差分が、下図になります。
折れ線グラフは、きれいな曲線です。
ヒストグラムは、一様分布のようにも見えますが、端の法が高くなっています。
Rによる対応のない２標本の類似度分析 のページがあります。
順路
次は
ネイマン・ピアソン流の検定
