Rによるデータ分析

Rによる対応のない２標本の類似度分析

対応のない２標本の類似度分析 です。

２標本の分布関数の作成

この段階は、 コルモゴロフ-スミルノフ検定 でも同じ作業をします。

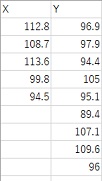
上のようなデータを、スタートとします。

library(tidyr)
setwd("C:/Rtest")
Data <- read.csv("Data.csv", header=T)
Data_long <- tidyr::gather(Data, key="Xs", value = Val) # ２列のデータを、１列にまとめる
Data_long2 <- na.omit(Data_long)# 欠損値のある行を削除
Data_long3 <- Data_long2[order(Data_long2$Val),]# 並び替え
Data_long3$Index = row(Data_long3)[,1]# 順位付け
Data_long4 <- Data_long3
n <- nrow(Data_long3)
Xno <- 0
Yno <- 0
for (i in 1:n) {
if(Data_long3[i,1] == "X"){
Xno <- Xno + 1
} else {
Yno <- Yno + 1
}
Data_long4[i,4] <- Xno# Xの累積度数
Data_long4[i,5] <- Yno# Yの累積度数
colnames(Data_long4)[4] <- "fX"
colnames(Data_long4)[5] <- "fY"
}
nX <- length(na.omit(Data[,1]))# Xのサンプル数
nY <- length(na.omit(Data[,2]))# Yのサンプル数
Data_long4[,6] <- Data_long4[,4] / nX# Xの経験分布の算出
Data_long4[,7] <- Data_long4[,5] / nY# Yの経験分布の算出
Data_long4[,8] <- Data_long4[,6] - Data_long4[,7]# 経験分布の差分
colnames(Data_long4)[6] <- "GX"
colnames(Data_long4)[7] <- "GY"
colnames(Data_long4)[8] <- "GX-GY"
Data_long4

２標本の分布関数の分析

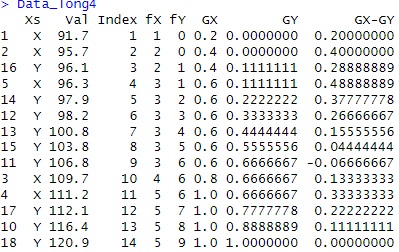
上で作ったデータをグラフにします。

元のデータのヒストグラム

library(ggplot2)
ggplot(Data_long4, aes(x=Val)) + geom_histogram() + facet_grid(Xs~.)

２つの累積分布の折れ線グラフ

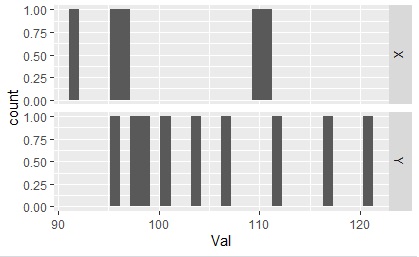
library(ggplot2)
Data_long5 <- Data_long4[,-8][,-5][,-4][,-2][,-1]
Data_long6 <- tidyr::gather(Data_long5, key="GName", value = GVal, -Index)
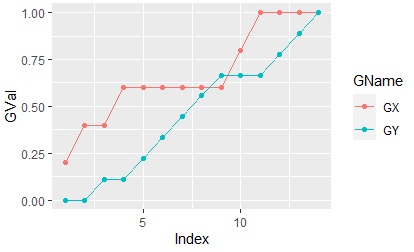
ggplot(Data_long6, aes(x=Index,y=GVal, colour=GName)) + geom_line() + geom_point()

累積分布の差分の折れ線グラフ

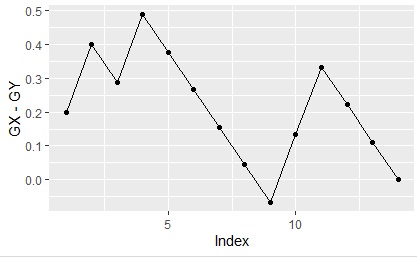
ggplot(Data_long4, aes(x=Index,y=GX-GY)) + geom_line() + geom_point()

累積分布の差分のヒストグラム

ggplot(Data_long4, aes(x=GX-GY)) + geom_histogram()

Rによるデータ分析