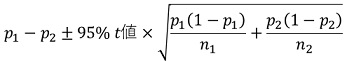
比率の差の効果量の検定は、 比率の全体的な差の検定 の一種です。
平均値の差の効果量の検定 と似ています。
平均値の差の検定の計算で使われている統計量は、ざっくり見ると、以下の形になっています。
平均値の差/(標準偏差/サンプル数nの平方根)
平均値の差の効果量の検定では、それを以下のようにします。
平均値の差/標準偏差
比率の差の効果量の検定も、これと同じ考え方をします。
比率は、これ自体が標準化されたような値(0から1で固定)なので、
効果量の信頼区間は、下記の式で良いような気がしています。
比率の差の検定
と同じ式です。
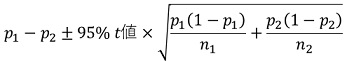
下記は、下側の求め方ですが、上側でも同様です。
EXCELの場合、例えば、比率がp1とp2の場合、下の式で効果量の信頼区間(下側)が求まります。
= ABS(p1-p2) - 1.96*(SQRT((p1*(1-p1)/n1 + p2*(1-p2)/n2)))
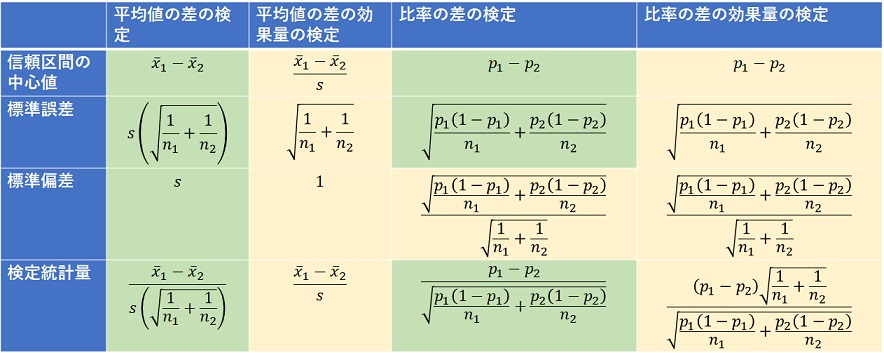
上の表で、緑色の部分の式は、教科書にのっているくらい有名な式です。
黄色の部分は、既存の式を眺めつつ、やりたいことができるための式を、筆者がアナロジーで出してみたものです。
EXCELの場合、例えば、p1、p2という2つの比率があり、それぞれのサンプル数がn1とn2の場合、下の式でp値が求まります。
=1-NORMDIST(ABS(p1-p2)*sqrt(1/n1+1/n2)/(SQRT((p1*(1-p1)/n1 + p2*(1-p2)/n2))), 0 , 1,TRUE)
上の表のそれぞれの計算式を、EXCELの計算式として入れています。 NORMDIST関数の最初の引数には、検定統計量が入ります。 2番目の引数は、平均値の差が0かどうかが基準になるので、0です。 3番目の引数は、標準偏差が入ります。
P値の信頼区間 は、効果量の信頼区間の上側と下側の値を、P値の計算式に入れて計算すれば良さそうです。
P値の計算の、ABS(p1-p2)の部分に、効果量の信頼区間の下側の式を入れます。
EXCELの場合、下の式でp値の信頼区間(上側)が求まります。
=1-NORMDIST(ABS(p1-p2) - 1.96*(SQRT((p1*(1-p1)/n1 + p2*(1-p2)/n2)))*sqrt(1/n1+1/n2)/(SQRT((p1*(1-p1)/n1 + p2*(1-p2)/n2))), 0 , 1,TRUE)
順路


 次は
比率分布の重なりの検定
次は
比率分布の重なりの検定

