分散比による重なりの検定は、 ばらつきの違いの全体的な検定 の一種です。
考え方は、 差による分布の重なりの検定 と似ています。 差による分布の重なりの検定 は、 平均値の差の検定 の代替手段として考案していますが、 分散比による重なりの検定は、分散の比の検定の代替手段として考案しています。
標準偏差のばらつきについては、特に心配しなくて良いくらいサンプル数が多い場合(目安としては30以上)に使える方法です。
分散比による重なりの検定は、分布のばらつき方の違いを調べる方法として、筆者が考案した方法です。 (世の中で、既に同じアイディアがあれば、ご存知の方は、ご教示いただけると幸いです。)
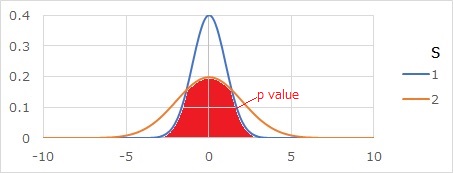
ばらつきの違いの全体的な検定のp値は、下のグラフの赤い部分です。
2つの分布が重なっている部分の面積になります。

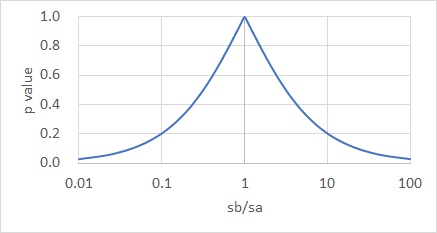
計算すると、下のグラフになります。
グラフの横軸は、2つの分布の標準偏差の比です。
2つの標準偏差が違うほど、小さな値になっています。
良く見る部分を拡大すると、下のグラフになります。
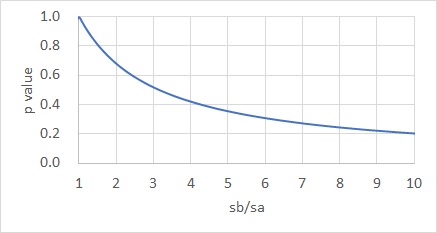
このp値は、一般的な検定のように、0.05を目安にするものではないです。 例えば、横軸が3の時に、p値は0.5くらいになりますが、「0.5(50%)もずれているから、2つのばらつきは違う、と考えられる」といった使い方になります。
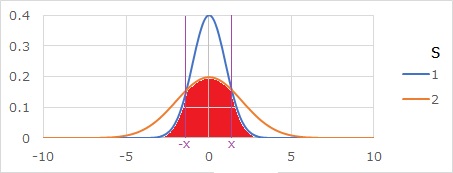
2つの分布が重なっている部分の面積ですが、まずは、確率密度関数の曲線の交点xを求めます。
確率密度関数の式に代入すると、下の式になります。
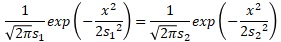
これを整理するとxの式が求まります。
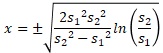
A2、B2というセルに2つの標準偏差が入力されている場合、EXCELでこのxを求める関数は、下記になります。
=-SQRT(2*B2^2*A2^2/(B2^2-A2^2)*LN(B2/A2))
上記のxを求める関数がD2というセルに書かれている場合、EXCELでp値を求める関数は、下記になります。
=2*(0.5-NORMDIST(D2,0,MAX(A2:B2),TRUE)+NORMDIST(D2,0,MIN(A2:B2),TRUE))
ここで、最初の「2*」という部分は、左側半分の面積だけを求めた式を2倍することを表しています。 「0.5」というのは、正規分布の左側半分の面積は、0.5なことを表しています。 MAX、MINというのは、2つの標準偏差の大小関係を間違えると、この式でp値が求まらないので使っています。 この関数だと、標準偏差がまったく同じ場合は、エラーになります。
順路


 次は
比率の全体的な差の検定
次は
比率の全体的な差の検定

