トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

P値と標準正規分布の関係

検定 において、P値は切っても切れないほどのものです。

ところが、P値がどのようにして計算されて来るのかは、あまり説明されないです。 検定統計量を求めることが説明されることはありますが、そこから先がどうなってP値になるのかが説明されることは、一般的ではないです。

一方、 標準正規分布確率の話は、よく知られています。 特に、製造業の中で、使われる統計学では、常識とも言えるようなものです。

P値の話は、標準正規分布の話とつながっているのですが、それを理解するには、検定では、 統計量の分布 を調べている点がポイントです。

標準正規分布と、統計量の分布の関係

ここでは、わかりやすい例として標準正規分布を使って説明します。

正規分布をしているデータについて、 標準化 をすると、 標準正規分布 になります。

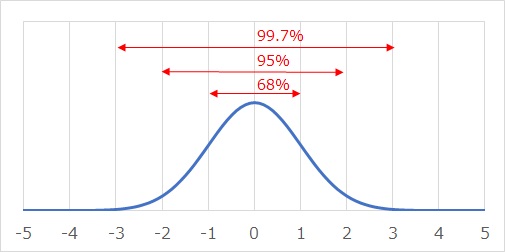
標準正規分布については、範囲と割合の関係がよく知られています。

ここで、統計量の検定の理論で重要なポイントなのに、あまり説明されないことがあります。 それは、統計量の検定で見ている分布が、 統計量の分布 なことです。

平均値の検定なら、上のようなグラフを使って見るのは、平均値の分布です。 平均値を計算するのに使った、データの分布ではないです。

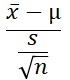
平均値の検定では、検定統計量は、上の式です。 この式と 標準化 の式の違いは、分母が

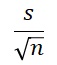
になっているところだけですが、この分母は、平均値の標準偏差を表しています。 ちなみに、平均値の標準偏差は、 標準誤差 と呼ばれています。

つまり、統計量の分布を見るために、分母の式が違いますが、平均値の検定は、広い意味での標準化をして、範囲と割合の関係を調べる理論になっています。

よくある誤解

一般的な解説では、検定統計量の式は出て来ても、nが入っている意味については説明しないのが普通のようです。 それもあり、「統計量の分布を調べている」という理解にはならず、 「データのばらつきに対して、統計量の確からしさを調べている」と言う誤解が多いようです。 （少なくとも、筆者自身は、長い間、この誤解をしていました。）

P値と標準正規分布の関係

ここまで準備できると、標準正規分布の、範囲と割合の関係の知識が役に立ちます。 P値として見ているのは、これらの範囲の外の割合です。 P値の目安は、0.05にすることが多いですが、この目安は、標準誤差が、-2から2までの範囲を見ていることに相当します。

実際の手法のバリエーション

上記では、正規分布を例にしましたが、実際の平均値の検定では、 t分布 を使います。

また、さらに他の検定では、違う分布を使うこともあります。 サンプル数が少なければ、特定の分布を使わずに、場合の数を求めて、割合を求め、これをP値として使う場合もあります。

サンプル数が多ければ、正規分布を仮定して、 z検定 として進める方法もあります。