有限の正規分布

数学的な正規分布と、実務の中の正規分布の大きな違いは、数学的な正規分布は範囲が無限なのに対して、実務の中の正規分布は有限になっているところです。

実際のデータの分布

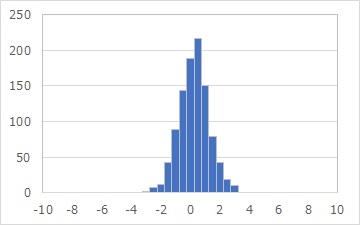
上のようなデータがあったとします。範囲が-3から3くらいまであって、正規分布のように見えます。

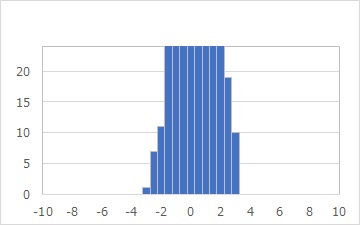
データ全体のグラフでは、分布の裾野がわからないです。拡大してみると、やはり-3から3くらいで、それ以上離れたところに、データはないことがわかります。

上の例では、データがマイナスの領域にもありますが、重さや長さのように、物理的にプラスの値しかあり得ないものものあります。

このようなデータでは、マイナスはあり得ないです。

「マイナスはあり得ないデータはどうなっているのか？」ということで、下のように、０のところで絶壁のようになっている正規分布をイメージする人がいるかもしれませんが、筆者は、このようなパターンを見たことはないです。

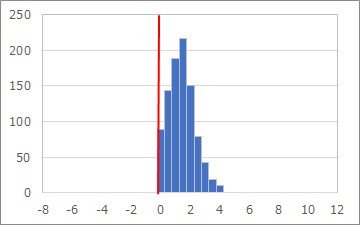
経験論ですが、プラスしかあり得ないデータの場合、プラスの領域に入るような形で、データが山の形で分布するのが普通です。

ところで、こういうデータに対して、「正規分布なのだから、例えば、100が出る確率は、ゼロではない。 100という数字がデータに含まれていないのは、確率的に非常に小さいからだ。膨大な数のサンプリングをすれば、出て来てもおかしくない」という考え方があります。

そういう考え方の根拠は、下のようになっています。「正規分布は、無限小や無限大の領域がある」というのが、根拠になっています。

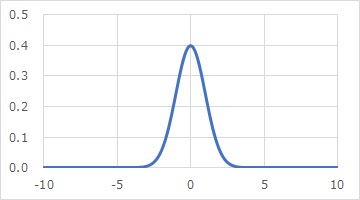
しかし、経験的に確かなのは、上のようなデータに対して、「正規分布の式を当てはめると、数学的な扱いがしやすくなる」という点だけではないかと思います。「データの背景には正規分布がある」という説には、根拠がありません。

極端に外れた値が表れない理由について、何にでも当てはまる普遍的な理由があるかどうかはわかりませんが、上のデータについては、理由があります。

上のデータは、乱数を発生させて作ったデータです。このようなデータは、有効数字があるので、限りなく0に近い値や、1に近い値を発生させた時に、有効数字によって近さの限度が決まっています。そのため、膨大な量の乱数を発生させても、極端に外れた値が作られることがないです。

統計的仮説検定や外れ値のモデルでは、ある程度以上外れた時に、「確率的に低いことが起きたのではなく、そもそも原因が違うことが起きたのだ」と考えることで判定をします。

この判断をする時に、「統計学は『確率がゼロである』とは言ってくれない」と考えると、不安になります。この不安が残ることで、意思決定に踏み切れない事もあります。

ところで、実務の正規分布は有限の範囲になることを踏まえると、「確率的に低いことが起きたのではなく、そもそも原因が違うことが起きたのだ」という話ではなくなり、「確率がゼロのことが起きたので、原因が違うのだ」という話になるので、不安はなくなるはずです。

「確率がゼロ」は、おそらく統計学だけでは導けないですが、条件次第では導けるのではないかと考えています。

順路次は統計量