 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
筆者の経験の範囲ですが、実務のデータ分析では、
正規分布
をよく使います。
ただし、きれいな釣り鐘型の正規分布を扱う訳ではないです。
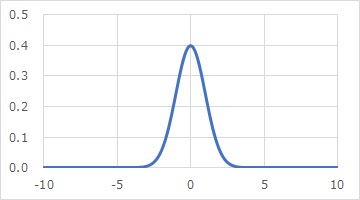
正規分布と、その他 のページで紹介している分布は、統計学の教科書でよく紹介されます。
実務のデータ分析では、「○○分布」と名前が付いているような分布とは違う方向で進める方が良いことがあります。 以下は、そういった話題です。
順路


 次は
正規分布から作られる分布
次は
正規分布から作られる分布

