単一分布と混合分布の見分け

データをグラフにして正規分布のような形に見えるようになるのは、少なくとも数十個はデータが必要です。

一方、統計学は数個程度のデータに対してでも、役に立つ理論です。数個程度の時は、正規分布に見えるようなデータではないのですが、実務の中の正規分布としては、このようなケースもよくあります。

スモールデータの考え方

上のような、n = 5のデータがあったとします。

こういうグラフを見ると、「上の２個と、下の３個に分かれている」ということに、気付く人が多いと思います。

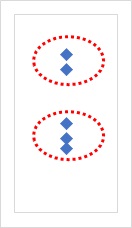
その次の考え方は、おそらく２通りに分かれます。

確率的な考え方をするのなら、「分かれているように見えるが、たまたま今回はこのパターンになったのだ。５個が集まるような時や、１個と４個に分かれるように見えることもあるはずだ。」となってきます。

データの背景を常に注意しているのなら、「上の２個と、下の３個は、測定の仕方とか、何かが違うのでは？」となってきます。

どちらなのかは、このデータだけでは判断できません。ここでのポイントは、まったく違う観点で、２つの可能性の仮説を立てるところになります。

筆者の経験では、上の例のようなデータの場合、上の２個と下の３個で、データの背景が違うことの方が、ほとんどです。

「測定した日が違う」、「測定器が違う」、「同一品種だが、ロットが違う」、といった違いが、違うことが多いです。

測定方法によりますが、工場で扱うような測定の場合、同じ条件で、短時間で全部測定した時には、近い値になることが多いです。「同じ条件」というところが、何か違っていると、離れやすい性質があります。