 Rによるデータ分析
Rによるデータ分析
 Rによるデータ分析
Rによるデータ分析
ここでは、周期性のあるデータの分析方法として、fft、差分、自己相関の3つを説明しています。
これら3つで同じこともわかるのですが、計算の仕方が違うので、違うことがわかることもあります。
library(ggplot2) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
n <- nrow(Data)# データの行数を取得
ft <- log10(abs(fft(Data[,1]^2)))# データの1列目をfft。出力の2乗の絶対値を抽出
Data2 <- as.data.frame(ft)# データフレーム形式に変換
Data2$Index <- as.numeric(row.names(Data2))# データの番号を付加
Data3 <- Data2[2:floor(n/2),]# 出力の上半分を抽出
Data3$Wavelength <- n *2 / (Data3$Index-1)# 波長を計算
ggplot(Data3, aes(x =Wavelength, y=ft)) + geom_line()+labs(x="Wavelength",y="Power")# グラフに出力
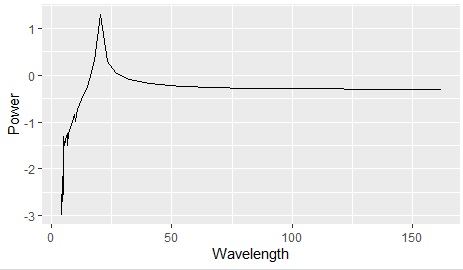
fftの出力は、上下で対称のものが出て、下半分は不要なので削除しています。
一般的には、fftの出力は周波(波長の逆数)を横軸にしますが、データの周期性を見たい時は、波長にした方がわかりやすいので、 ここでは波長(Wavelength)にしています。
上の図では、20行おきに周期性があることがわかります。 元のデータは下図のものです。確かに20行おきの周期性があります。
また、上の図だと、横軸が160くらいですが、データ数は約80です。
この160というのは、80*2から決まっています。
このため、横軸を見るとデータ数もわかります。
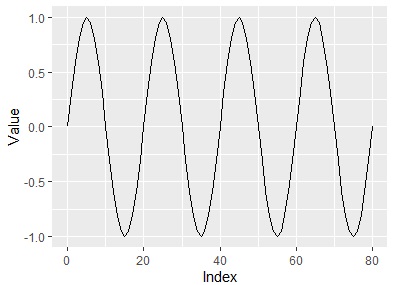
フーリエ変換の場合は、このページの他の2つの方法とは異なり、統計的な処理をしていないです。 そのため、1、2周期分しか入っていないような長い波長の場合でも、周期性の有無を調べることができます。
同じ列のデータの前後のデータの差(差分)を見る方法です。
library(ggplot2) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data_diff <- diff(Data[,1])# 差分を計算
Data_diff <- as.data.frame(Data_diff)# データフレーム形式に変換
Data_diff$No <-as.numeric(row.names(Data_diff))+1# データの番号を付加
ggplot(Data_diff, aes(x =Data_diff)) + geom_histogram()# グラフに出力
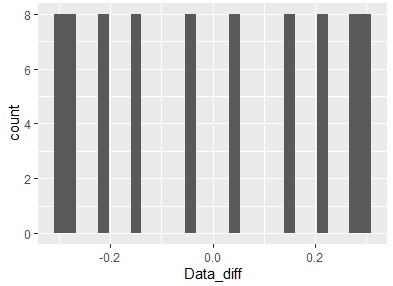
この例ではわかりにくいのですが、折れ線グラフにすると、sin波でひとつ前のデータとの差分を取ると、cos波になっていることがわかります。
ggplot(Data_diff, aes(x = No,y=Data_diff)) + geom_line()# グラフに出力
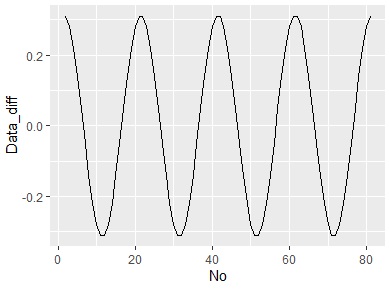
差分の場合は、差分の全部の組合せを直接データとして見ることができるので、差分の変化や、分布を見ることができます。
この例のデータは、20行おきに周期性がありますが、20行おきで差分をとってみます。
diff関数の中に「,20」と書くことで、20行おきの計算になります。
library(ggplot2) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data_diff <- diff(Data[,1],20)# 差分を計算
Data_diff <- as.data.frame(Data_diff,20)# データフレーム形式に変換
Data_diff$No <-as.numeric(row.names(Data_diff))+1# データの番号を付加
ggplot(Data_diff, aes(x =Data_diff)) + geom_histogram()# グラフに出力
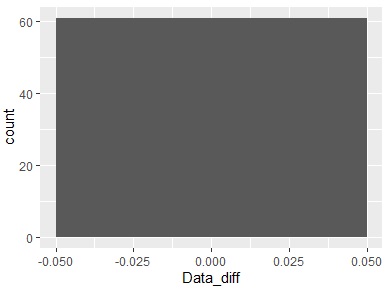
20行おきで差分を計算するので、差分は60個できます。 縦軸が「60」なので、すべての差分が同じ値になっていることがわかります。 横軸の中心が0なので、すべての差分が「0」になったこともわかります。 よって、20行おきに周期性があることが、差分からもわかります。
このように、差分を見ることで、周期性を分析することができます。
ひとつ前のデータとの差分からは、周期性はわからないので、周期性の分析をする時に、ひとつ前のデータとの差分は見ないのですが、 ひとつ前のデータとの差分も使い道があります。
ひとつは、 速度データ としての使い方です。 ひとつ前のデータとの差分には、「単位時間あたりの変化量」という物理的な意味があるので、 その見方でデータ分析をする時に使えます。
特に、ひとつ前のデータとの差分の分布がランダムなら、 ランダムウォークモデル を考えることもできます。
自己単相関分析 ができます。 同じ列について、1行ずらしたデータ、2行ずらしたデータ・・・、というようにして、それぞれについて相関係数を計算した結果が出ます。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
acf(Data[,1])# 自己相関を計算し、コレログラムを出力
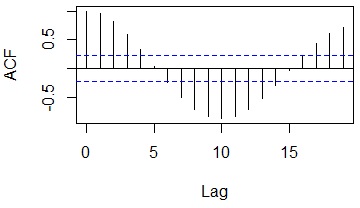
この例の場合は、10行ずらすと、負の相関が一番強く、20行ずらすと、正の相関が一番強いらしいことがわかります。
一般的な相関分析では、同じ行同士のデータを使って、異なる2列のデータの相関を調べます。
相互相関というのは、この分析方法に、「行をずらす」という観点も加えたものです。 「時間的な遅れがあるので、片方の列をずらすと相関が高くなる」というケースを調べることができます。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
ccf(Data[,1],Data[,2])# 1列目と2列目の相互相関を調べる
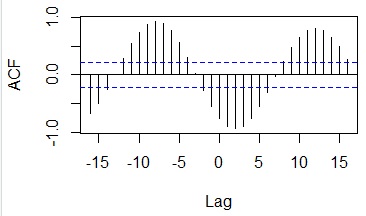
この例の場合は、7個ずらすと、非常に相関が高くなることがわかります。
差分だと、いくつ行をずらすとデータの見通しがよくなるかを調べるのに、片端から調べる必要があります。 コレログラムを使うと、この作業があっという間に終わります。
上記の、差分やフーリエ変換では、異なる2列のずれの分析はできないです。
同志社大学 金明哲先生のページ
Rによる自己相関、相互相関、差分
https://www1.doshisha.ac.jp/~mjin/R/Chap_33/33.html

