クラスター分析 は、グループの作り方で方法が大きく分かれ、階層型と非階層型があります。 「階層型がボトムアップ、非階層型がトップダウン」と言っても良いかもしれません。
階層型の方法は、各サンプル間の距離を見て、近いもの同士でグループを作っていく方法です。 デンドログラムと呼ばれるトーナメント表のようなグラフが作られ、これが階層的なグラフになっています。
グループ分けは、この階層型のグラフの情報を使って進めます。
近さの指標には、様々なものが考案されています。
非階層型では、出力が階層になりません。
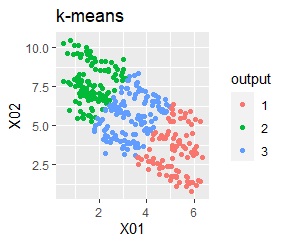
k-means法では、例えば分析者が「k = 3」と指定すると、グループが3つになるように、サンプルを分けます。
X-means法は、k-means法と似ていますが、kを自動的に決めてくれるところが違います。
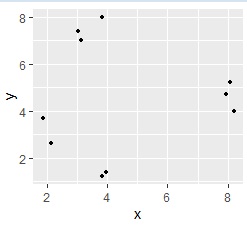
ただし、思ったような数には、なかなかならないようです。 下記のRを使った例では、「3」になると理想的なのですが、「8」になりました。
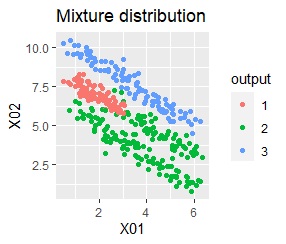
k-means法では、明らかにグループの中心に近いサンプルと、遠いサンプルが、同じように扱われます。 しかし、遠いサンプルは、他のグループに所属する可能性もわかるようにしておいた方が良いことがあります。 この時は、混合分布を使うと、複数のグループへの所属の可能性が確率的にわかります。
DBSCANは、近いもの同士でグループ分けをするので、グループの中心点というものがありません。 そのため、複雑な形でも対応できます。
もうひとつ特徴があり、「グループには属さないサンプル」という判定もしてくれます。
HDBSCANは、階層型とDBSCANの中間のような方法です。 結果も両方の特徴があります。
下記は、 Rによるクラスター分析 のページのコードを使ったものです。
２変数（２次元）のデータについて、データの違いに対して、手法の違いがどのように表れるのかをまとめています。 散布図にした時に、人が目で見てわかるグループの違いを、クラスター分析の手法も同じように抽出できるのかを見ます。
DBSCANを使いやすくするために、データは正規化してから分析しています。
結論を先に書くと、以下になります。
３つのグループがあります。どれもばらつきは同じくらいです。
階層型（ward.D2とsingle）と、k-means法、混合分布法（Mixture distribution）では、k=3としています。
例1Aの場合は、どの方法でも人が目で見てわかるグループの違いを、クラスター分析の手法も同じように抽出できています。
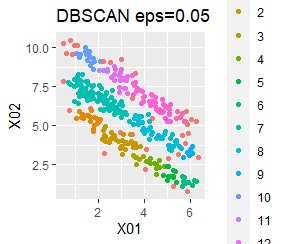
ただし、DBSCANでepsが小さ過ぎると、外れ値(0のグループ)と判定されるものが出て来ます。 大き過ぎると、２つのグループが１つと見なされています。
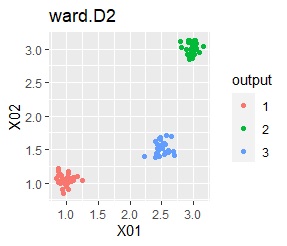
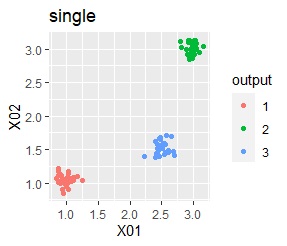
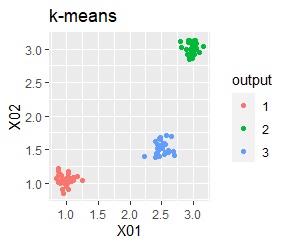
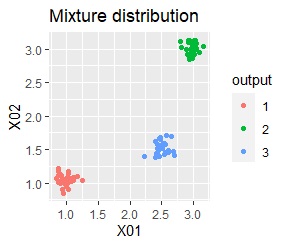
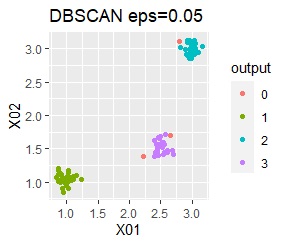
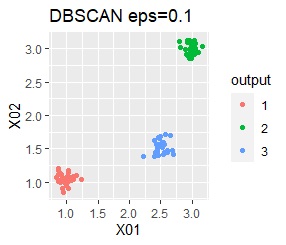
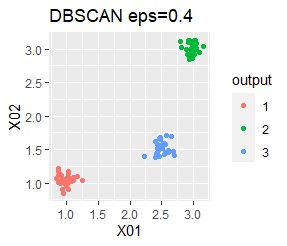
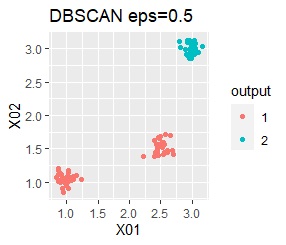
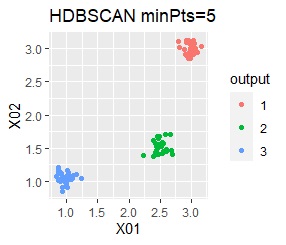
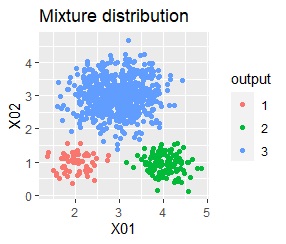
３つのグループがあります。どれもばらつきは同じくらいです。 例1Aとの違いは、３つのグループの境界付近にもデータが複数あり、グループの境界がはっきりしていない点です。
階層型（ward.D2とsingle）と、k-means法、混合分布法（Mixture distribution）では、k=3としています。
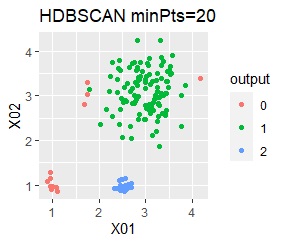
３つのグループをうまく分けることができたのは、ward.D2、k-means、Mixture distributionでした。 singleとDBSCANはダメでした。 HDBSCANは、minPtsが20で外れ値と３つのグループに分かれています。 これはこれで正解ですが、扱いが難しい感じです。
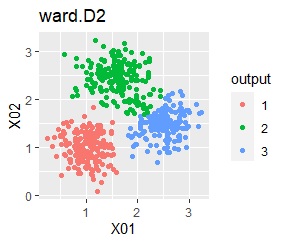
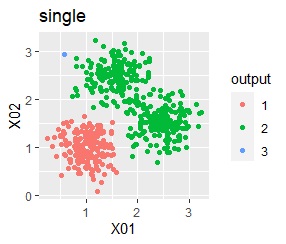
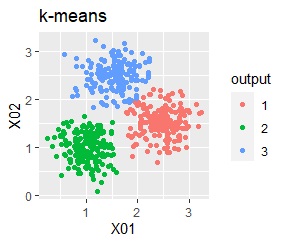
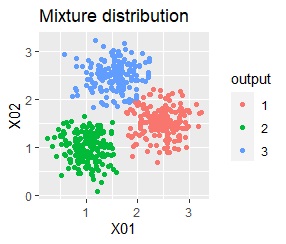
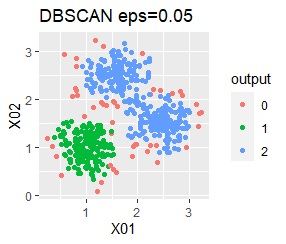
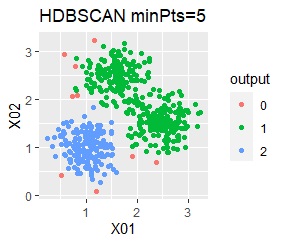
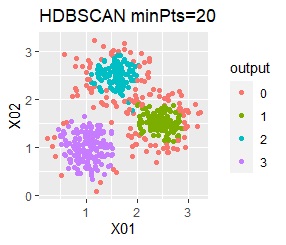
３つのグループがあります。１つのグループは、ばらつき方が大きいです。
階層型（ward.D2とsingle）と、k-means法、混合分布法（Mixture distribution）では、k=3としています。
例2Aの場合は、ward.D2、single、Mixture distribution、DBSCAN eps=0.2、HDBSCANでは、理想的な判定ができています。
k-meansだと、ばらつきの小さなグループの一部が、大きなグループの一部と見なされています。 これは、k-meansがすべてのグループの大きさを同じと見なすところから来ています。 なお、この例では、この性質が結果の悪さの原因になっていますが、場合によっては、この性質を分析に利用することもできます。
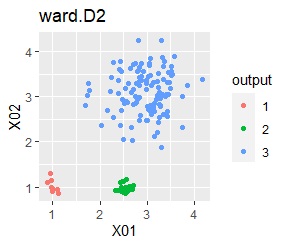
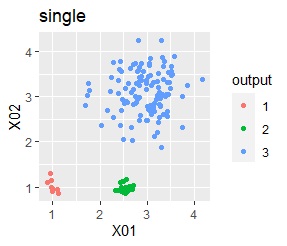
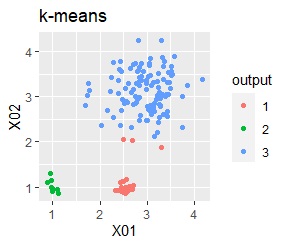
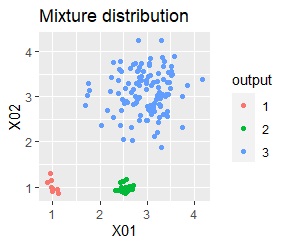
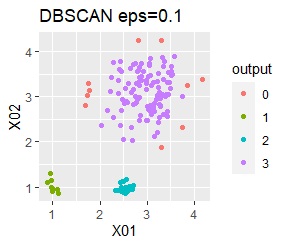
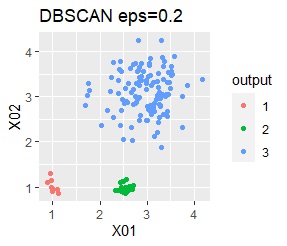
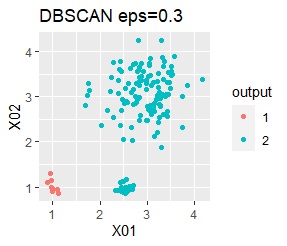
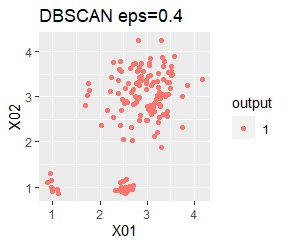
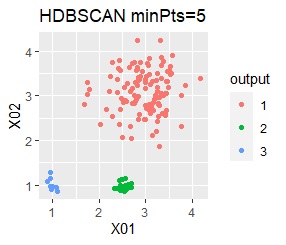
３つのグループがあります。１つのグループは、ばらつき方が大きいです。 例2Aとの違いは、３つのグループの境界付近にもデータが複数あり、グループの境界がはっきりしていない点です。
階層型（ward.D2とsingle）と、k-means法、混合分布法（Mixture distribution）では、k=3としています。
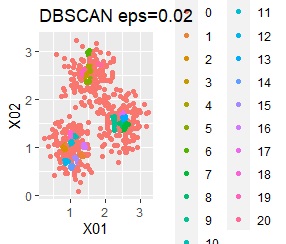
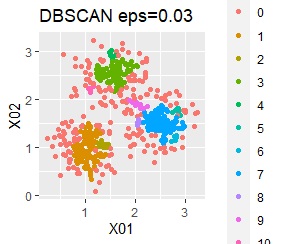
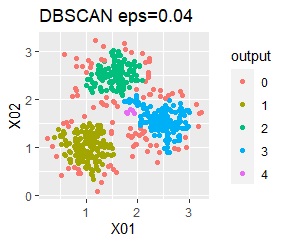
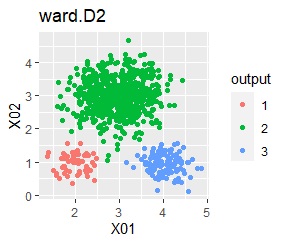
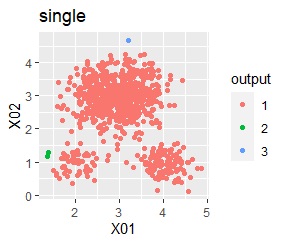
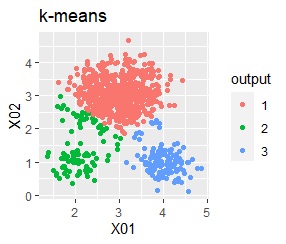
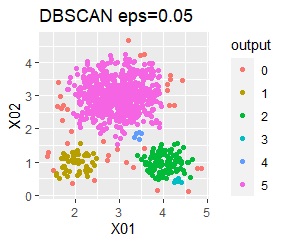
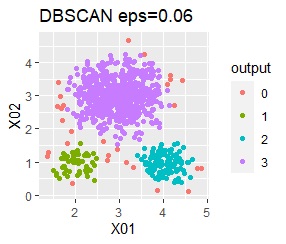
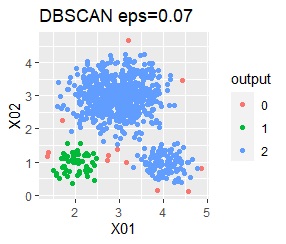
例2Bの場合は、ward.D2、Mixture distribution、HDBSCANでは、理想的な判定ができています。 それ以外はダメでした。
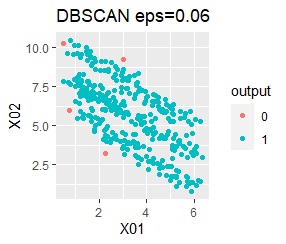
DBSCAN eps=0.06の場合は、３つのグループは抽出していて、グループの境界付近だけはグループ0に分類しています。 どのグループに属するのかがはっきりしないものは、別に扱えるのは、これはこれで使い道があります。 ただ、この例のようなシンプルなものでも、epsを0.01刻みで変えて初めて出せるようなものですので、実務で使える技ではなさそうです。
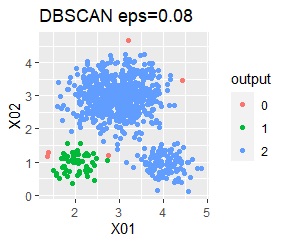
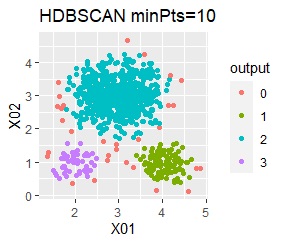
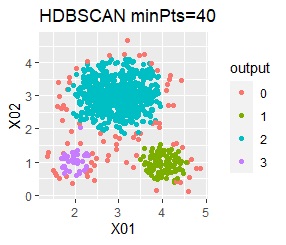
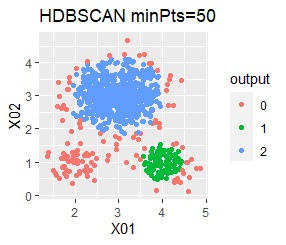
直線状にサンプルが並んでいる３つのグループがあります。境界ははっきりしています。
階層型（ward.D2とsingle）と、k-means法、混合分布法（Mixture distribution）では、k=3としています。
single、Mixture distribution、DBSCAN eps=0.1、HDBSCAN minPts=5では、理想的な判定ができています。
ただし、DBSCANはepsを0.01刻みで結果がだいぶ変わるので、実務で使える技ではなさそうです。
HDBSCANはひとつのグループに含まれるサンプル数よりも、かなり小さい値にしないと、うまく分かれないです。 扱いが難しい感じです。
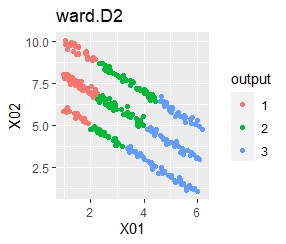
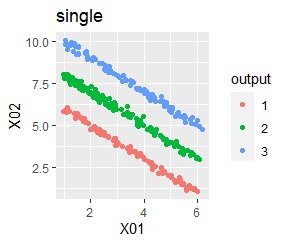
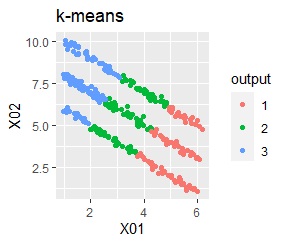
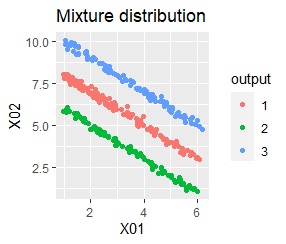
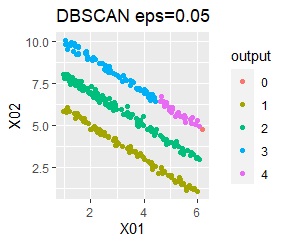
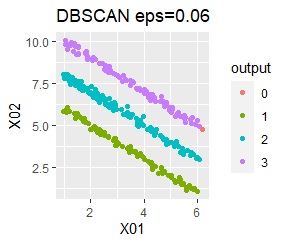
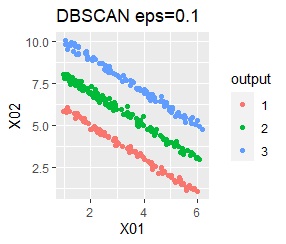
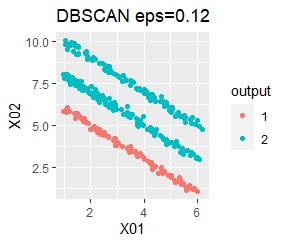
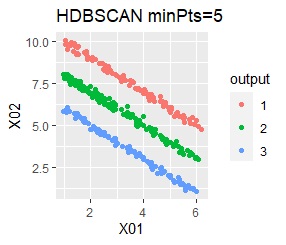
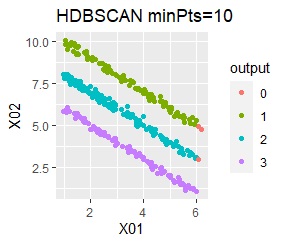
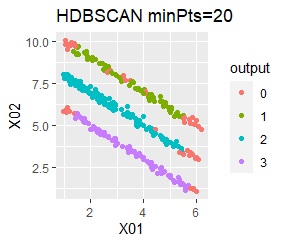
直線状にサンプルが並んでいる３つのグループがあります。 例3Aとの違いは、サンプルの数で約16倍あります。
階層型（ward.D2とsingle）と、k-means法、混合分布法（Mixture distribution）では、k=3としています。
singleとDBSCANで、理想的な判定ができています。 例3Aと違って、Mixture distributionはダメでした。 DBSCANとHDBSCANでは、理想的な判定になるパラメタの幅がそれなりに広いので、実務で使える感じです。
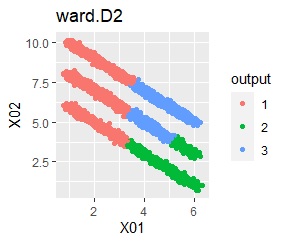
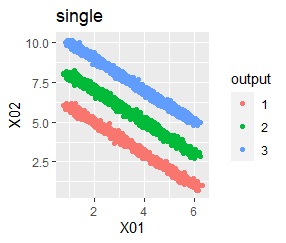
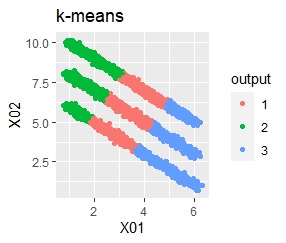
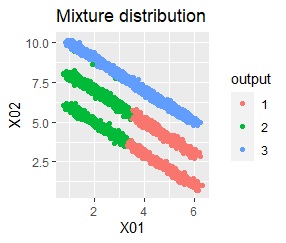
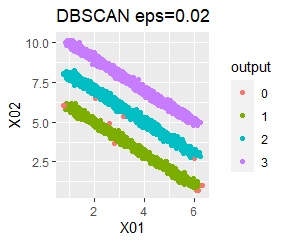
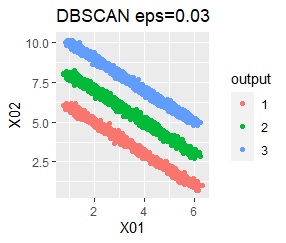
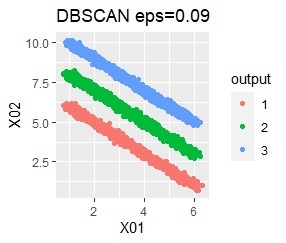
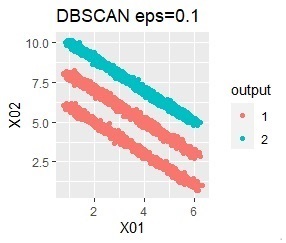
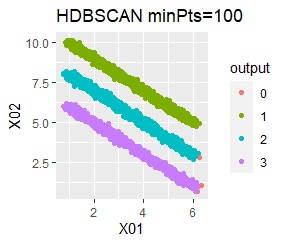
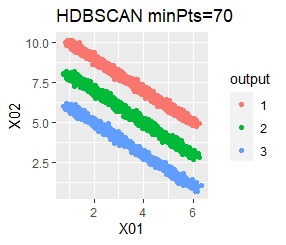
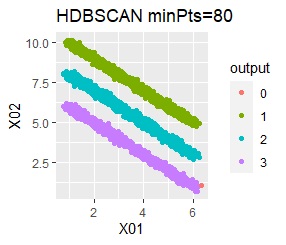
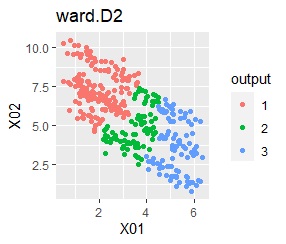
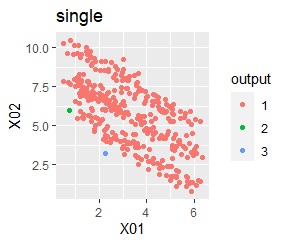
直線状にサンプルが並んでいる３つのグループがあります。 例3Aとの違いは、３つのグループの境界付近にもデータが複数あり、グループの境界がはっきりしていない点です。
階層型（ward.D2とsingle）と、k-means法、混合分布法（Mixture distribution）では、k=3としています。
全部ダメでした。
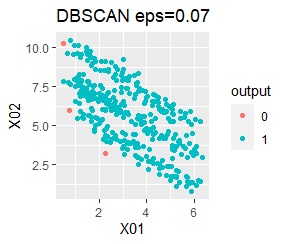
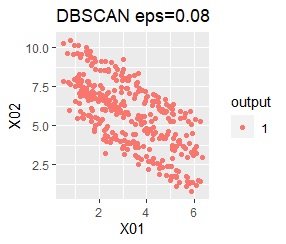
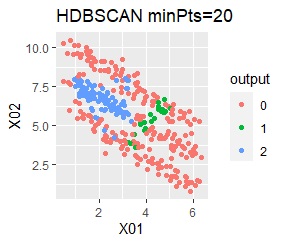
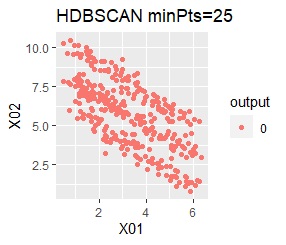
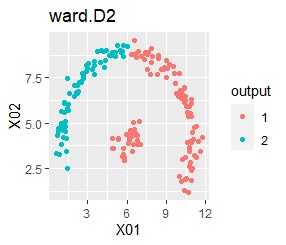
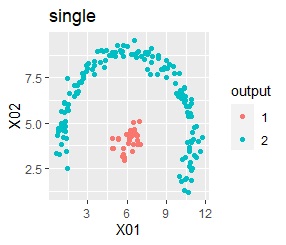
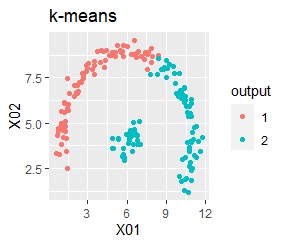
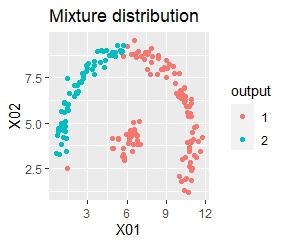
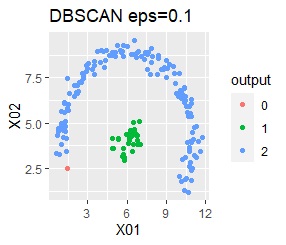
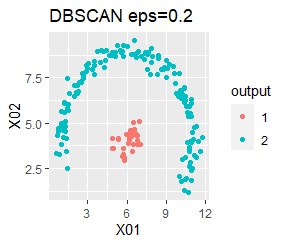
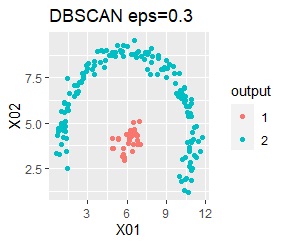
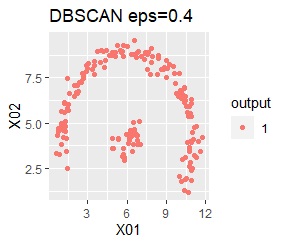
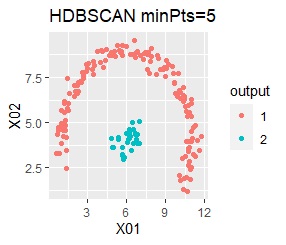
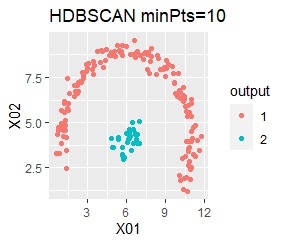
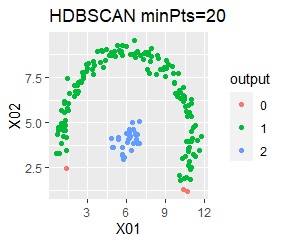
２つのグループがあります。１つのグループは、円弧状になっています。
階層型（ward.D2とsingle）と、k-means法、混合分布法（Mixture distribution）では、k=2としています。
single、DBSCAN、HDBSCANで、うまく判定できています。
ward.D2、k-mean法、Mixture distributionは、特殊な形のグループを扱えないことがわかります。
このページで紹介している方法の中で、X-means法と、DBSCANは、最終的なグループの数が自動で決まるのは良いのですが、 X-means法だと思ったような数になりにくい問題がありますし、DBSCANはパラメータの設定の難しさがあります。
階層型、k-means法、混合分布法では、適切なグループ数（k）を指定すれば、各サンプルはわりと適切に振り分けてくれる良さがあります。
ところが、適切なグループ数の設定が難しいです。 階層型なら、デンドログラムから見積もることができます。 また、データが2変数（2次元）なら、 ２次元散布図 を見れば、見積もることができます。
データが3変数以上の場合は、2変数の時のように ２次元散布図 を使って手軽にグループの数を見積もる方法として、 高次元を２次元に圧縮して可視化 を使って、分析のデータを2変数のデータにしてしまう方法が考えられます。
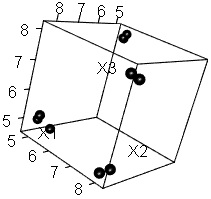
下の図は、3次元空間上に4つのグループがあることがわかっているデータが左で、
自己組織化マップ
で2次元にしてみた結果が右です。
4くらいが適当なことは、見当が付きます。
DBXCANでは、近さの判断に「eps」というパラメータを使います。 これをうまく設定すると、グループ数が適切になります。
3次元以上の場合や、変数ごとに単位が違う場合、パラメータepsの設定が難しいです。
この対策として、
(x - min)/(max - min)
という式を使い、
それぞれのデータを、それぞれの変数のmaxとminを使って、0から1のデータに収まるようにする方法があります。
こうすると、どのようなデータなのかがわからないデータでも、変換したデータではepsが1より大きいものが必要になることはなくなります。
データの空間をある程度分割できるグループのサイズとして、epsは0.1から0.3くらいに設定すれば良いかと思います。
ただし、各変数のもともとの値の大きさが重要な場合は、この方法は使えません。
Rによる実施例は、 Rによるクラスター分析 のページにあります。
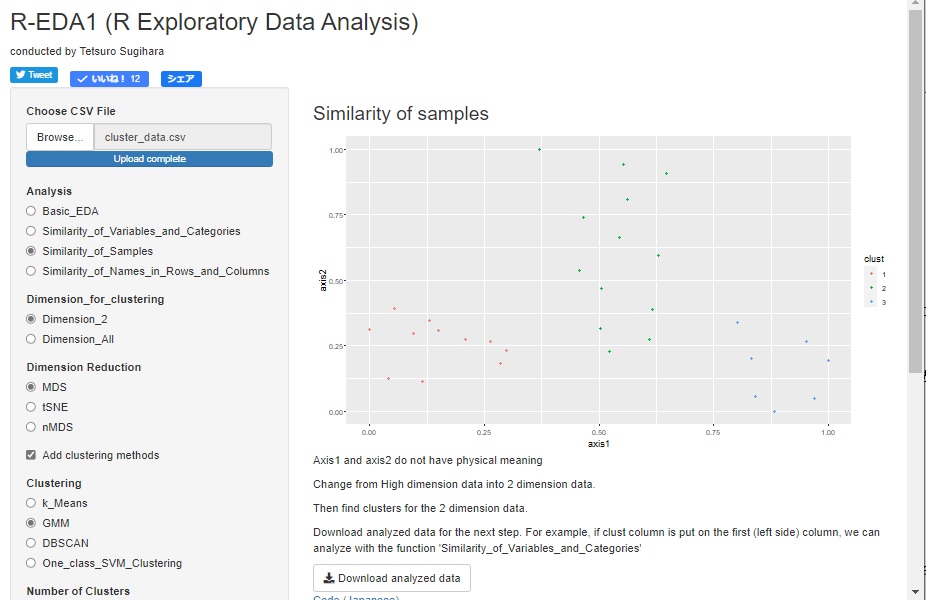
R-EDA1 では、k-Means法、混合分布法、DBSCANを使えます。 クラスタリングの結果を元のデータに追記したデータをcsvファイルで出力できるので、 このデータを今度は入力データとして使うと、ラベル付きデータとして分析することもできます。
k-Means法と混合分布法については、高次元を二次元にする方法を使って、二次元散布図で表せるようにしてから、 その後のグループ分けの方法として使えるようになっています。 二次元になっているので、kはグラフを見ながら決められます。
DBSCANについては、k-Means法や混合分布法と同じ目的の使い方と、高次元のままグループ分けする方法としての使い方の両方ができるようになっています。
「Python実践AIモデル構築100本ノック」 下山輝昌・中村智・高木洋介 著 秀和システム 2021
様々な手法について、使い方がコンパクトにまとまっています。
k-means：エルボー法は残差平方和で最適なkを推定。シルエット分析はクラスタ内の密度と、クラスタ間の距離で最適なkを推定
階層型クラスタリング：最短距離法、最長距離法、群平均法
MinBatchMeans：k-meansを少ないサンプルで実行することで計算時間を短縮
MeanShift：kの設定が不要。k-meansベースで、近いクラスタはひとつにしていく。
x-means：kの設定が不要。k-meansベースで、ひとつのクラスタを正規分布２つに分けるべきかで判断して、必要なら分ける。
GMMクラスタリング：複数の正規分布を仮定して、どれに近いのかを判断
VBGMMクラスタリング：kの設定が不要。GMMをベイズ推定で実行してkを決めて行く。
SpectrumClustering：密度でクラスタを形成
DBSCAN：密度でクラスタを形成。外れ値も出せる。
HDBSCAN：DBSCANとは異なり、塊ごとの密度の違いに対応する。DBSCANだと、密度の薄い塊は外れ値が出て来やすいが、それが起きない
「Pythonで動かして学ぶ!あたらしい機械学習の教科書」 伊藤真 著 翔泳社 2018
Pythonを使った計算自体も、自分で作る人向けの教科書になっています。
教師なし学習
として、k-means法と、混合ガウスモデルを紹介。
混合ガウスモデルは、k個の中心と、その中心から広がる正規分布で、確率的にクラスターを判定できる。
k-means法と違って、各点は、どれかひとつのクラスターに所属するのではなく、複数のクラスターのそれぞれに対しての、確率的な所属の仕方がわかる。
「フリーソフトではじめる機械学習入門」 荒木雅弘 著 森北出版 2014
機械学習
全般の本ですが、ニューラルネットワークから、ディープラーニングまでの流れがコンパクトにまとまっています。
k-means法だけでなく、kが自動的に決まるx-means法も紹介。
k-means法の弱点として、分散が一定な点を挙げ、分散が中心毎に異なるモデルとして、混合分布による確率密度推定を紹介。
「Pythonではじめる機械学習 scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎」 Andreas C.Muller, Sarah Guido 著 オライリー・ジャパン 2017
Pythonを使った機械学習について、具体的な話がコンパクトにまとまっています。
k-means法は、丸くないクラスタを識別できない。
この本では、階層型クラスタリングを、「凝集型クラスタリング」という名前でも呼んでいる。
k-means法のようにクラスターの数を分析者が与える必要がなく、かつ、どのクラスターにも属さない点を判別できる方法としてDBSCANを紹介。
DBSCANも、階層型クラスタリングと同様に、予測に使えない。
「Pythonではじめる教師なし学習 機械学習の可能性を広げるラベルなしデータの利用」 Ankur A.Patel 著 オライリー・ジャパン 2020
言葉による説明とPythonの実施例は出てきますが、数式は出てこない本です。
時系列クラスタリングとして、心電図データのクラスタリングが出てきます。
心電図データには、スケール変換やシフト変換がありますが、k-Shape法はこれらの変換に影響されない距離の尺度を使うので、適しているそうです。
ただし、k-平均法やHDBSCANも全然ダメという訳ではないそうです。
「データマイニング入門 ：Rで学ぶ最新データ解析」 豊田秀樹 編著 東京図書 2008
データマイニング
の入門書です。
また、これらの手法をRでやってみるための手引書にもなっています。
クラスター分析の手法は、階層型とk-means法が紹介されています。
Rで実行する時のポイントとして、この本では、データを「scale」関数に入れて、
標準化
する方法を紹介しています。
このページでは、標準化ではなく、0から1の区間に収まるように変換しています。
単位系の異なる変数を合わせるだけでなく、DBSCANのepsの考えやすさから、標準化にはしませんでした。
順路
次は
２次元散布図を使ったクラスター分析
