 Rによるデータ分析
Rによるデータ分析
 Rによるデータ分析
Rによるデータ分析
クラスター分析 は、 データマイニング の手法として、よく知られています。 ここでは、その使い方の紹介になります。
Rを使ったクラスター分析の実施例になります。 クラスター分析の手法は、いろいろありますが、共通部分は一緒に書いています。
下記は、コピーペーストで、そのまま使えます。 下記のコードを使った場合、X-means以外は、このページの一番上にある色分けのグラフと同じ結果になります。 この例では、入力データは量的データになっていることを想定しています。 質的データがあるとエラーになります。
以下に、複数の方法がありますが、入力データの作り方は同じなので、ここにまとめています。
この例では、Cドライブの「Rtest」というフォルダに、 「Data1.csv」という名前でデータが入っている事を想定しています。
入力データの読み込みをします。
Data10からData11への変換は、すべての列を0と1の間のデータにするためのものです。
DBSCANをする時はあった方が良いですし、どの手法だとしても、身長と体重など、単位が違う変数が混ざっている場合は必須です。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data1 <- read.csv("Data1.csv", header=T) # データを読み込み
Data10 <- Data1[,1:2]## クラスター分析に使うデータを指定。ここでは1〜2列目の場合
Data11 <- Data10 # 出力先の行列を作る
#以下の3行は、前処理としてデータを正規化する場合は必要
for (i in 1:ncol(Data10)) { # ループの始まり。データの列数を数えて同じ回数繰り返す
Data11[,i] <- (Data10[,i] - min(Data10[,i]))/(max(Data10[,i]) - min(Data10[,i]))
} # ループの終わり
#以下の2行は、前処理としてデータを主成分にする場合は必要
pc <- prcomp(Data11, scale=TRUE,tol=0.01) # 主成分分析
Dat11 <- as.data.frame(pc$x)# 寄与率の高い主成分を抽出
階層型はいろいろありますが、非階層型のk-means法や混合分布法と近い結果になる方法で一番使いやすいのがウォード法で、 DBSCANと近い結果になるのが最近接法なので、下記はその2つを例にしています。
library(plotly)
library(ggdendro)
Data11_dist <- dist(Data11)# サンプル間の距離を計算
hc <- hclust(Data11_dist, "ward.D2") # ウォード法による階層型クラスター分析
#plot(hc)# 一般的なデンドログラム
ggplotly(ggdendrogram(hc, segments = TRUE, labels = TRUE, leaf_labels = TRUE, rotate = FALSE, theme_dendro = TRUE))# 拡大可能なデンドログラム
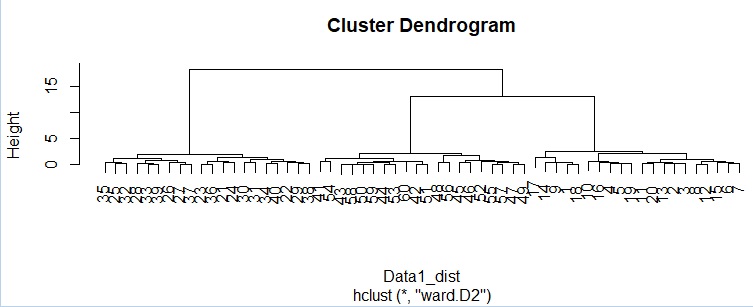
デンドログラムから、狙い通りに3つのグループに大きく分かれている様子がわかります。
最近接法では、「single」にします。
hc <- hclust(Data11_dist, "single") # 最近接法による階層型クラスター分析
この例は、データが60個なのでできなくもないのですが、サンプルが多い時は、
デンドログラムから各サンプルがどのように分かれるのかを読み取れなくなります。
結果をデータとして出力する方法ですが、
各サンプルを3つのグループに分けると、どのグループに所属するのかは、下記のようにすると出力できます。
output <- cutree(hc,k=3)# 3個にグループ分け
km <- kmeans(Data11,3) # k-means法で分類。これは3個のグループ分けの場合
output <- km$cluster # 分類結果の抽出
X-means法の使い方は、k-means法と似ていますが、ライブラリのインストールが事前に必要です。 また、細かいところが少し違います。
library(clusternor) # ライブラリを読み込み
Data11 <- as.matrix(Data11) # データを行列に変換
xm <- Xmeans(Data11,10) # X-means法で分類。最大のグループ数を10個に指定。
output <- xm$cluster # 分類結果の抽出
library(mclust) # ライブラリを読み込み
mc <- Mclust(Data11,3) # 混合分布で分類。これは3個のグループ分けの場合
output <- mc$classification # 分類結果の抽出
DBSCANは、epsの設定が悩みどころになりますが、前処理で正規化していれば、データの範囲は最大で1なので、 グループの範囲の目安は、0.1から0.3くらいで良いはずです。
library(dbscan) # ライブラリを読み込み
dbs <- dbscan(Data11, eps = 0.2) # DBSCANで分類。epsは、コア点からの距離の範囲です。ここでは、0.2にしました。
output <- dbs$cluster # 分類結果の抽出
HDBSCANでは、epsの設定はしなくても良いのですが、minPtsを設定しないとエラーになります。 minPtsは、核になるクラスタを構成するサンプルの数で、これが小さいと、細かいクラスタができやすくなります。
library(dbscan) # ライブラリを読み込み
dbs <- hdbscan(Data11, minPts = 5) # HDBSCANで分類。minPtsは、グループのサンプル数の最小値。
output <- dbs$cluster # 分類結果の抽出
Rには、クラスター分析用のグラフのパッケージもありますが、ここでは汎用的な ggplot2 を使う例になります。
library(ggplot2) # パッケージの読み込み
Data <- cbind(Data1, output) # 最初のデータセットにグループ分けの結果を付ける
Data$output <-factor(Data$output) # グループの変数を文字列型にする
Data$Index <-row.names(Data) # Indexという名前の列を作り、中身は行番号にする
ggplot(Data, aes(x=X1, y=X2)) + geom_point(aes(colour=output))# 二次元散布図 色分け・形分け
ここで、下のデータのようにデータが少ない場合は、行番号をプロットする方法も便利です。
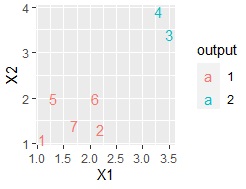
ggplot(Data, aes(x=X1, y=X2,label=Index)) + geom_text(aes(colour=output))# 言葉の散布図
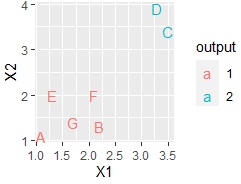
各サンプルの名前の列がある場合は、それを使うこともできます。
ggplot(Data, aes(x=X1, y=X2,label=Name)) + geom_text(aes(colour=output))# 言葉の散布図
write.csv(Data, file = "Output.csv") # データをcsvファイルに出力

