21世紀の、相関係数の検定

21世紀の検定としての、相関係数の検定を、このページで整理します。

相関係数の検定では、相関係数を、検定対象、効果量、寄与率で共通して使います。共通しているので、分けて説明する必要がないのですが、他の検定の準備として、他の検定と同じ分け方で、このページは説明しています。

検定対象

相関係数は、２つの変数の共分散を、２つの変数の標準偏差の積で割った量です。

相関係数の信頼区間は、以下になります。

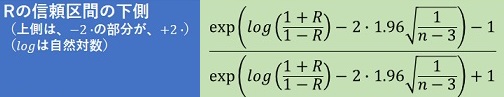
実務では、信頼区間として知りたいのは、相関係数がどのくらいまで低い可能性があるのかなので、以下では、信頼区間の下側について説明します。このページの他の信頼区間についても同様です。

相関係数の信頼区間の下側の具体的な計算は、以下になります。 R1セルに相関係数、N1セルにサンプル数を入力しておくと、以下の関数はコピペで使えます。
r1　：　相関係数
n1　：　サンプル数

= ( EXP(LN( (1+r1)/(1-r1) ) -2*1.96/SQRT(n1-3) ) -1) / ( EXP(LN( (1+r1)/(1-r1) ) -2*1.96/SQRT(n1-3) ) +1)

=T.DIST.2T((ABS(r1)*SQRT(n1-2)/SQRT(1-r1^2)), n1-2)

P値の信頼区間は、p値を求める式に、相関係数の信頼区間の下側を入れる案を、さしあたって考えてみました。

相関係数の信頼区間の下側をR2セルに入力しておくと、以下の関数はコピペで使えます。

=T.DIST.2T((ABS(r2)*SQRT(n1-2)/SQRT(1-r2^2)), n1-2)

相関係数の検定の場合、効果量は相関係数です。

検定対象の信頼区間は、そのまま効果量の信頼区間にもなります。

相関係数の２乗は、寄与率としての意味を持っています。

相関係数をR1セルに入力しておくと、以下の関数はコピペで使えます。

=r1^2

寄与率の信頼区間（上側）です。寄与率を求める式に、相関係数の信頼区間の下側を入れます。

相関係数の信頼区間の下側をR2セルに入力しておくと、以下の関数はコピペで使えます。

=r2^2

相関係数の検定のo値のページにまとめています。

「相関係数」　BellCurve
https://bellcurve.jp/statistics/course/9591.html?srsltid=AfmBOoqa6-P_7C2gdCj3YsVpvE8wu01RHpbLPdc1Z55IUaZHTfOi-xYu

相関係数について、検定や、信頼区間が示されています。