相関の検定

検定は、相関係数にもあります。

相関の検定の使い道

ここでは、p値が0.05（有意水準5%）を目安として、それよりも大きいか、小さいかを見ることにしています。

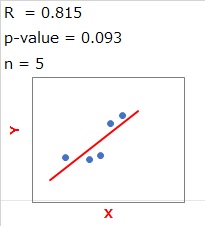
correlation
上の図は、サンプル数が5個です。相関係数は0.815で、散布図を見ると、だいたい一直線上に並んでいます。

このような時に、「相関がある！」とすぐに結論を出さずに、「相関があるのかもしれないけれど、断定するのは危ないかも」、という判断をする時に、p値は、0.093で0.05より大きいというのは参考になります。

このように、相関係数がある程度大きくても、用心深く考えたい時に、p値は参考になります。

サンプル数が1000個で、相関係数が0.1の時の散布図が下になります。
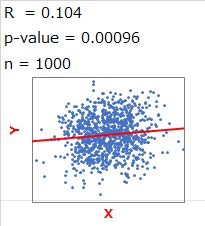
correlation

この図を見て、「XとYには、何か意味のある関係がある」とは思う人はいないと思いますが、「p値が小さいというのは、何か意味がある時」という理解をしていると、「何か意味があるのでは？」と思えてしまいます。

つまり、「p値がとても小さいので、相関係数が小さいけれども、何か意味のある関係がある」、という使い方はできないです。

相関係数の検定のp値は、相関係数という量の、データの確からしさを表しています。

p値が小さければ、小さいほど、計算した相関係数は確からしいことを表します。

このp値は、相関性を表していないです。そのため、「p値がとても小さいので、相関係数が小さいけれども、何か意味のある関係がある」、という使い方はできないです。

下の図は、サンプル数によって、p値がどのように変わるのかを表しています。
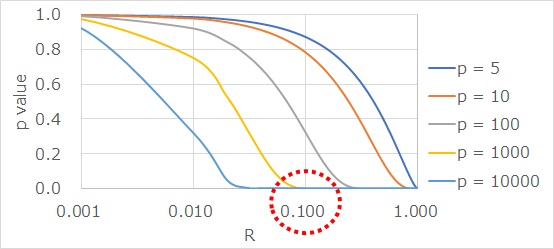
correlation

サンプル数が1000個の場合、相関係数が0.1のような時でもp値はかなり小さいことがわかります。

相関係数の検定として知られている方法は、相関係数として計算した数字の、確からしさを評価する方法です。そのため、データ全体の相関性を見ている訳ではないです。

相関係数の効果量の検定のページでは、従来からある検定は、統計量の確かさを評価する方法で、データ全体に対して、統計量がどのような位置付けなのかについては評価してないことを書いています。そして、データ全体に対して、統計量がどのような位置付けなのかについて評価する方法を、新しく提案しています。

そのページにも書きましたが、相関性について、「データ全体」という視点で評価して、かつ、検定のようにP値で評価する方法は、
(1 - 相関係数の２乗)
が活用できます。

「生物統計学」　米沢勝衛　他　著　朝倉書店　1988
相関係数の検定や、相関係数の信頼区間があります。

「無相関の検定―相関係数の有意性を検定する」　BellCurve
https://bellcurve.jp/statistics/blog/14324.html

エクセルを使ってp値を出す計算式があります。