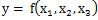
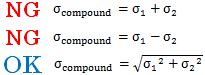
Errors are expressed by the standard deviation. If we want to study the effects of the sum of unevenness, the calculation of the sum of standard deviations is wrong.
The collect calculation is the square root of the sum of the square of the standard deviations.
If there is correlation between the errors, this calculation is not enough correctly. But, in my experience, the difference is too small to be the problem of my analyisis.
If Y is a function of three Xs, general formulation is
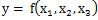
If "e" is the error of T and each X, the error of the Y is function that
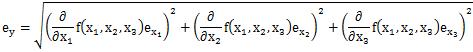
The formulations of the error of the combination of variable are not same. This is called " Propagation of Errors."
The error of formulation of the sum, (X1 + X2), is calculated by
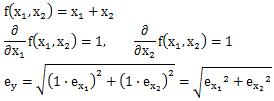
This forrmulation is same of "Caution of the Calculation with Standard Deviation" above.
The formulation of the difference is same to the formulaion for the sum. And this formulation is useful as the application of Paired t-test.
The formulation of the error of the area of the square is
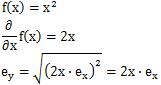
Generrally, the formulation of the propagation of errors is different from the square root of the sum of the square of the standard deviation.
