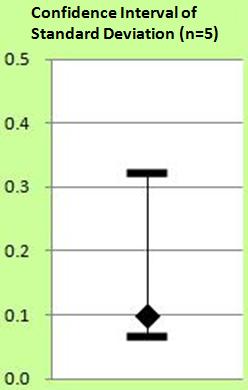
The right figure means that "Confidence Interval is between 0.07 and 0.32."
Standard deviation is an important index to evaluate dispersion.
Conclusion is that
"n = 5 is enough in many cases to evaluate average. But about n =50 is needed to evaluate standard deviation in many cases."
There is a formulation to calculate the confidence intervals of variance as well as confidence intervals of averages. By using Excel for 95% confidence,
Upper = n * Variance / CHIINV(0.975,n-1))
Lower = n * Variance / CHIINV(0.025,n-1))
"0.975" and "0.025" are calculated from the number "95%
".
0.975 = 1 - (1 - 0.95) / 2
0.025 = (1 - 0.95) / 2
In this site, I use the formulation below.
The basic idea is that
Square root of variance = Standard Deviation.
By using Excel for 95% confidence,
Upper = SQRT(n * Standard Deviation^2 / CHIINV(0.975,n-1)))
Lower = SQRT(n * Standard Deviation^2 / CHIINV(0.025,n-1)))
The right figure means that
"Confidence Interval is between 0.07 and 0.32."
It means that the difference between 0.1 and 0.2 is useless.
The difference between 0.1 and 0.2 seems big because 0.1 is the half of 0.2. So "useless" is important information to decide next approach of analysis.
This is idea is also useful to evaluate process ability.
The right figure tells us the relationship between n and the intervals.
This figure tells us that "more than 10 are needed".
And it also tells that the effects of numbers between 20 and 30 are not so different. So if there is big data of samples, the difference between 0.010 and 0.012 is not valuable to study.
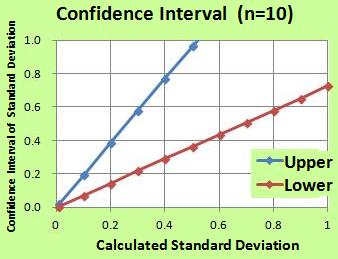The right figure tells us the relationship between calculated standard deviation and the intervals.
The bigger the standard deviation, the wider the intervals.
If there is a set of standard deviation from 0.1 to 0.6, there is not useful difference among the numbers of standard deviation.
In my experience, more than 100 are hopeful to evaluate the difference of standard deviation.
NEXT 
Use of Double Measured Data
