The "estimate" on this page is a statistical estimate. It is an important theory that supports Hypothesis Testing.
There are statistics such as mean and standard deviation, but these calculations are statistically called "point estimates."
It is more difficult to think about than point estimation, but there is also a "interval estimation". It is a way to estimate the range of a statistic with a certain probability. The interval estimate for the mean is the confidence interval.
Point estimates and confidence intervals are estimates of statistics.
More information about confidence intervals can be found on the Confidence intervals and standard errors page.
Prediction intervals are estimates of individual data.
Prediction intervals can be used to Model of Outlier and Model of Abnormal but not Outlier.
Academically, confidence intervals seem to attract more attention than prediction intervals. Perhaps because of this, there is software that has the function to calculate confidence intervals but does not calculate prediction intervals, but not vice versa. More information about prediction intervals can be found on the Prediction intervals page.
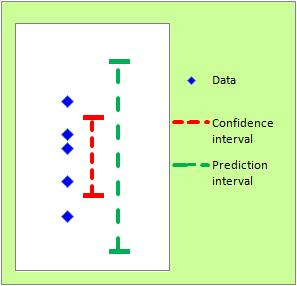
When there are 5 samples, the confidence interval and the prediction interval are calculated at 95% each, as shown in the graph below.
The confidence interval indicates the location of the mean. The prediction interval shows the extent of the data.
Strength and Weakness of Big Data
NEXT 
Confidence intervals and standard errors
