トップページ |
統計学の解釈学 |
このサイトについて
トップページ |
統計学の解釈学 |
このサイトについて
以下は、筆者の私見です。 誤解があれば、ご教示いただけると幸いです。
ARモデル は 時系列分析 の教科書で必ずと言って良いほど紹介されます。
筆者が実際のデータでARモデルの係数を求めると、いくつかパターンがあるようなのですが、そうしたことについて、説明している文献は見当たりませんでした。
そこで、筆者はできるだけ体系的に調べることにしました。 詳細は、 多項式とARモデルの関係 、 ばらつきとARモデルの関係 、 周期性とARモデルの関係 、 三角関数とARモデルの関係 のページに分かれています。 このページは、これらのページからわかることを総合的にまとめたものです。
規則は、ばらつきが非常に大きい場合と、ばらつきがない場合が両極端になるようです。 それらの中間くらいの場合は、中間のような値になります。
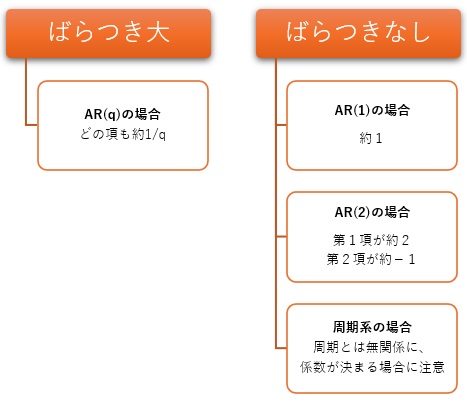
この部分は、主に ばらつきとARモデルの関係 からの知見です。
ばらつきが大きい場合というのは、全体的には増減の様子が見られるものの、隣接した値は、必ずしも近くない場合です。
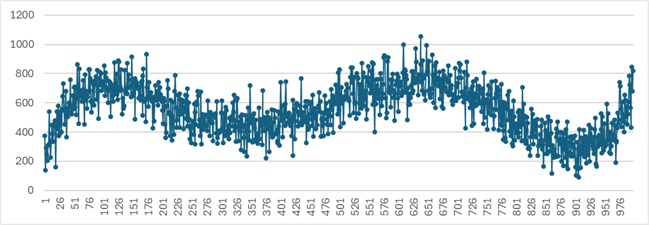
上記の例で、AR(5)、つまり、５個前のサンプルまで遡るARモデルを作ると、係数は、
0.18、0.14、0.13、0.25、0.21
になります。
合計は0.91です。
この例の場合は、 移動平均モデル に近いものが求まっています。
この例よりも、ばらつきが大きくなればなるほど、合計は０に近付いて行きます。
この例よりも、ばらつきが小さくなって、５次の多項式に近くなると、係数は０よりも小さくなったり、１よりも大きくなったりします。
この部分は、主に 多項式とARモデルの関係 からの知見です。
ばらつきがない場合というのは、隣接した値が、非常に近い値になっていて、グラフでは、曲線のようにプロットが並ぶ場合です。
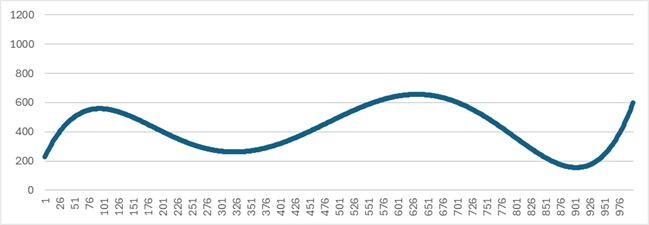
上の例の場合は、５次の多項式で完全に近似できます。
ここで話が唐突ですが、５次の多項式までの場合は、ARモデルの係数が、ほぼ確実に求まります。
「ほぼ」というのは、「２次式に近い３次式」のような場合は、この規則が当てはまらないためです。
上の式は、上から順に、１から５次の多項式です。
上の式は、例えば、２行目の場合、任意の２次の多項式は、AR(2)の係数を求めると、
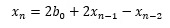
という式になることを表しています。
ポイントは、b0以外は、AR(2)の式の中に入っていないことです。 多項式の時と、ARモデルでパラメーターの数が異なるように見えますが、ARモデルの場合は初期値に依存するため、初期値もパラメーターに加えると、パラメーターの数は一致します。
上記も含めて、さらに複雑な場合もまとめると、下記の表のようになります。
まず、AR(1)の場合は、切片以外の係数は、ほぼ１になります。 上記の例の場合は、1.000014です。
AR(2)以上も含めると、 切片以外の係数の合計が、ほぼ１になるのは、ばらつきが大きい場合と同じです。
１次式にほぼ一致する場合と、２次式にほぼ一致する場合は、それぞれ該当する多項式の係数になります。
それ以外の一般の曲線では、切片のところ以外の係数が、２次式の係数に近い値になります。
例えば、７次の多項式に一致するデータについて、AR(2)の係数を求めると、切片はデータによって大きく異なりますが、それ以外の部分については、
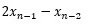
に近い値が求まります。
AR(3)以上ARモデルについて、係数を求める場合の考え方は、AR(2)の時と同様です。
この部分は、主に 周期性とARモデルの関係 からの知見です。
一般的な曲線は、多項式で近似できるので、多項式についての規則は、一般的な曲線の場合にも当てはまります。ただし、一般的な曲線の中でも、周期曲線は特別なことがあります。
下の例は、周期が12の周期曲線です。
12個前が、まったく同じ値になっています。
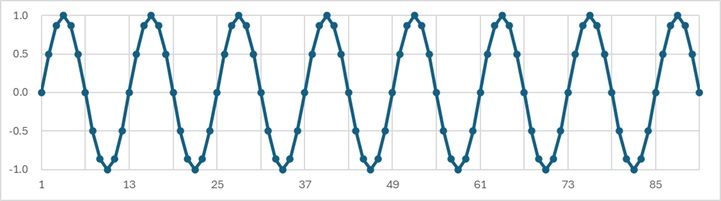
上の曲線について、AR(1)からAR(20)までの係数を、それぞれ求めると、下表になります。
AR(1)からAR(3)までの係数を求めると、下のようになります。
上の表で、「L=2」の行と、係数の決まり方が似ています。 理由は不明ですが、経験的に、上記のように周期的な曲線は、２次式の時の係数のパターンが当てはまります。
、AR(12)の係数を求めると、下のようになります。
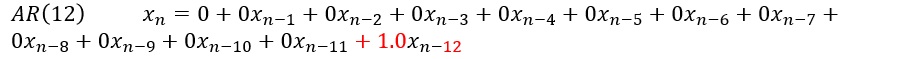
Xn-12の係数が1で、他が０でも成り立ちそうですが、そうはならないです。
例えば、AR(15)の場合は、下のようになります。
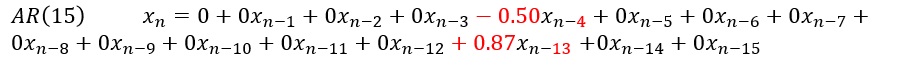
この場合も周期とは関係のないところで係数の値が決まっています。
このサイトには、 変数の重要度の分析 のページがありますが、一般的には、多変量解析をしてから、モデルの係数を見て、 「この変数の影響が大きい」といった考察をします。
ところが、ARモデルでは、このような考察ができません。
間違いがわかりやすい例ですが、 例えば、上記で周期が12の曲線に、AR(15)を適用すると、12とは関係のある項の係数が０で、他が０にならないです。 この結果だけを見ると、「5と14の周期があるのだ」と考えたくなりますが、 このように考察するのは、明らかに間違いです。
逆に例えば、4次式にほぼ一致する曲線に、AR(5)を適用すると、上の表から下記の結果になります。
この結果を見て、「２個前のサンプル以外は、関係するのだ」と考えても、あまり意味がありません。
ARモデルの係数は、個別ではなく、セットで見るものです。
上の例では、周期曲線について、AR(2)やAR(3)の係数を見て、「２次式と局所的に似ている」という考察をしています。 このように、係数のセットを見て、４次式までのどれに近いのかを考察するのは正しいです。
周期性を調べたい場合は、ARモデルの係数ではなく、自己相関を「１つ前のサンプル」、「２つ前のサンプル」と遡って調べていく、コレログラム分析をすると、間違いがないです。
