平滑化したランダムウォークモデルになるARモデル

以下は、筆者の私見です。誤解があれば、ご教示いただけると幸いです。

ARモデルは時系列分析の教科書で必ずと言って良いほど紹介されます。

このページでは、ARモデルについて、筆者が気が付いたことを説明します。先行研究があるかもしれませんが、筆者は見かけたことがないです。

それは、「ARモデルは、ランダムウォークモデルを平滑化したもの」という点です。

仮説の検証の仕方

平均が０、標準偏差が１の乱数を、約10000個作ります。

それらを使って、ARモデルの代表的な２つのタイプで仮説を検証しています。

ひとつのタイプは、ARモデルの係数がすべて同じで、かつ、係数の合計が１になる場合です。このページでは、このタイプを「AR(q)」と呼ぶことにします。一般的には、「AR(v)」と書く時は、vは、項の数を表しますが、ここで使うqは、項の数だけでなく、係数の計算に使う分母も表します。

もうひとつのタイプは、指数平滑法です。ここでは、指数平滑法を直近のデータほど重みを付けたARモデルとして使います。「ES」と呼ぶことにします。
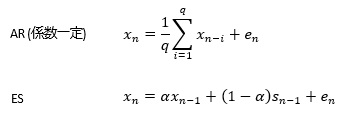
平滑化したランダムウォークモデルになるARモデル

AR(1)と、ES(α=0)は一致します。これらは、ランダムウォークモデルと同じです。

ARでは、qが増えるほど、ESでは、αが増えるほど、ランダムウォークモデルよりも変動が小さく、滑らかな変化をしています。このページのタイトルの「平滑化」は、この様子を表現しています。

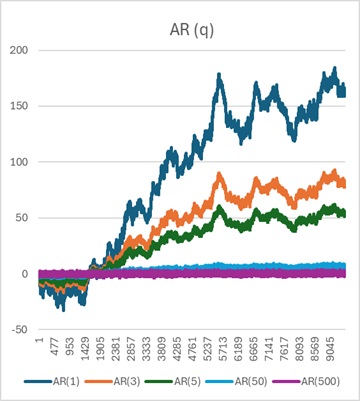
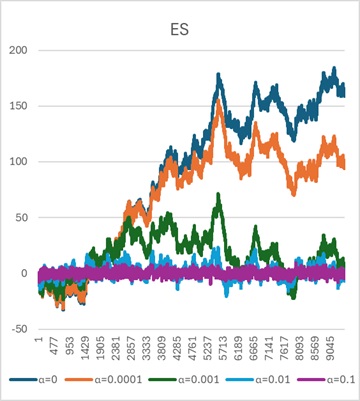
平滑化したランダムウォークモデルになるARモデル

qやαが増えるほど、０の近傍を推移するようになります。この理由は、乱数の平均が０であるためです。

qやαが増えるほど、遠い過去の乱数との平均を計算する形になるため、０に近付きます。

MAモデルは、項が増えるほど、遠い過去の乱数との平均を計算する形になるため、乱数の平均が０なら、０に近付きます。この点が、ARモデルと似ています。