トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
ARモデル ほどではないのですが、MAモデルも 時系列分析 の本で紹介されることが多いモデルです。
MAモデルのMAは、「Moving Average（移動平均）」の略です。 そのため、 移動平均モデル と名前が同じになるのですが、こちらは「MAモデル」と呼んで区別することが一般的です。 このサイトでも、この呼び方で区別します。
下の例は、MAモデルの例です。
MA(20)というのは、20個まで時点を遡っていることを表します。
一見すると、 ARモデル と見た目が似ています。 明らかに違うのは、中心になる値の有無です。 ARモデルでは、中心になる値がないので、シミュレーションすると、全体的に増加傾向や、減少傾向になることも起きます。 MAモデルの場合は、この例の場合は、中心が10で、10からは離れ過ぎないようにして、増減しています。
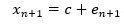
MAモデルの前に、上の式を考えます。
この式は、「n+1番目のxは、一定値cにn+1番目の誤差が加わったもの」ということを表しています。
例えば、誤差が正規分布なら、「xは、平均値がcの正規分布」ということを表している式になります。
下の式がMAモデルの式です。
上の式との違いは、n+1番目のxの値の誤差に、n番目とn-1番目の誤差も含んでいる点です。
上の式では、n+1番目とn番目のxが近い値になりにくいのですが、下の式では、共通の値を含むので、近くなりやすくなっています。
移動平均モデル や ARモデル は、観測した値の移動平均について作られている理論です。 観測した値があって、その移動平均を計算して活用していきます。 移動平均は、計算して求める量です。
一方、MAモデルは、観測していない値の移動平均について作られている理論です。 この点が大きな違いになっています。
「観測していない値」というのは、誤差です。 式では「e」と書いている部分です。
MAモデルについて、ARモデルのように理解するのなら、係数bのある項が名前の通りの、移動平均（MA）になっています。
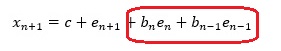
しかし、MAモデルを理解するには、eのある項をまとめてひとつのように考えた方が良いようです。
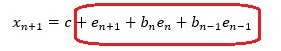
例えば、毎日入荷があって、入荷したものは翌日に半数、２日後に４分の１、３日後に０になるのなら、在庫量は以下の式で表せます。
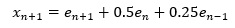
そのため、これと似た現象は、MAモデルに近くなると考えられます。
上記では、MAモデルの例として、在庫量のモデルを説明しました。 しかし、実際の在庫量がこのように減っている倉庫は、おそらくないので、あくまで想像上のモデルです
MAモデルが想定するデータは、基準になる値があって、そこから増減します。 増減しているものは、少ないデータを集計することによる誤差です。
世の中には、品質のデータや、位置のデータなど、人や機械が制御することによって、基準に近くなるように維持されている現象があります。
こうした現象のデータは、「基準になる値があって、そこから増減」という点では、MAモデルが想定しているデータと似ています。 しかし、上記のようなグラフではなく、「高くなって来たから、下がるように操作」といったことがわかるようなグラフになります。 「誤差」のような感じにはならないです。
MAモデルを紹介している文献はありますが、MAモデルが合う現実の現象を紹介している文献に、筆者は出会ったことがないです。 また、筆者の経験の範囲でも、そうした現象は出会ったことがないです。
ARモデルの場合は、１行ずらしたデータと、２行ずらしたデータを変数として、重回帰分析をすることで、係数aが求まります。 そのため、Excelでも簡単にできます。
MAモデルの場合は、重回帰分析ではできませんが、Excelの場合は、ソルバーを使った最適化計算でできます。 具体的には、eについての、二乗平均平方根誤差（RMSE）が最小値になるように、係数b、cを最適化する計算になります。 詳細は、 ExcelでMAモデル のページにあります。
順路
次は
SARIMAXモデル
