実線が生存率で、点線が信頼区間です。
生存時間分析は、 時間解析 の一種です。 扱う時間が「生存時間（寿命）」の時に、生存時間のデータから知りたいことを調べられるようになっています。
名前は「生存時間」ですが、生存時間分析の方法は、文字通り「生存時間」の分析の他に、 「薬の効き方」、「イベント発生までの時間」、「故障までの時間」、「退会までの時間」といった時間の分析にも使えます。 さらには、「長さ」のような物理量を扱う方法として、時間以外にも、応用が広げられる方法です。
生存時間分析では、このようなデータから、 「〇〇時間後の生存率」、「条件による寿命の違い」、「瞬間死亡率は増加傾向か？」、といったことが調べられます。
生存時間分析のデータには、独特の特徴があります。
生存時間は、一般には「寿命」とも呼ばれます。 「寿命」の場合は、生物だけでなく、工業製品にも使われます。
生存時間分析の基本は、複数のサンプルの生存時間という、１次元データの分析になります。
生存時間のデータは、測定開始と測定終了の時刻の差として求まります。 例えば、「生まれた・死んだ」が開始と終了の時刻です。 また、「入会・退会」、「服用開始・効き目が出た」、「使用開始・故障」等も、開始と終了にすることができます。
「途中で来院しなくなったので、経過がわからなくなった」、「長過ぎるので測定をやめた」、「実験期間が終わった」等の理由で、 開始は記録しているけれども、終了が記録されていないデータが発生することがあります。 こうしたデータは、「打ち切りデータ」と呼ばれます。 打ち切りデータは、 欠損値 の一種です。
打ち切りがあったとしても、打ち切りの時刻が記録されていれば、その打ち切りデータは、「その時刻までは生存していた」というデータにはなります。 生存時間分析には、打ち切りデータも活用できるようになっている方法もあります。
打ち切りがある場合とない場合が混ざったデータの場合、「時間」と「打ち切りの有無」の２つが必要になります。 そのため、打ち切りがあると、２次元データの分析になります。
分析の目的によっては、条件の違いで生存時間に違いがあるのかを調べたいことがあります。 その場合、条件を示す変数が必要になるので、３次元以上のデータになります。
A、Bという2人がいて、Aが2年で退会、Bが3年で退会したとします。
このデータを使うと、 1年目の生存率は1.0、2年目の生存率は0.5、3年目以上の生存率は0.0という計算ができます。
生存率は、生存関数と呼ばれます。
S(t)
と書きます。
上記の例だと、
S(1) = 1.0
S(2) = 0.5
S(3) = 0.0
S(4) = 0.0
といった使い方になります。
ある瞬間の瞬間死亡率（瞬間故障率）は、「ハザード関数」と呼ばれています。
h(t)
と書きます。
ハザード関数の一番簡単な形は、定数の時です。 例えば、「0.1」で1日を単位としたデータでしたら、この意味は、「1日当たり壊れていないものの10台に1台が壊れる」になります。 その時に壊れていないものの中の内訳を表しています。 そのため、「1日に0.1だから、10日で全部が壊れる」という計算にはなりません。 １日ごとに、その時に壊れていないものの中で、どうなっていくのかを表しています。 全体の数は、指数関数の逆数の形になって来ます。
ハザード関数h(t)の、時刻0からある時刻までの積分は、累積ハザード関数と呼ばれています。
H(t)
と書きます。
ハザード関数を「瞬間死亡率」と上記で書きましたが、累積ハザード関数は死亡率ではないです。
累積ハザード関数と生存関数（生存率）には、
H(t) = -log(S(t))
や
S(t) = exp(-H(t))
という関係があります。
死亡率 = 1 - 生存率
なので、だいぶ違います。
「生存時間の平均値」は、持っているデータに対してひとつ求まります。
一方、生存率は、だんだん変化する性質がありますので、持っているデータに対してひとつが求まるようなものではないです。 上記の、A、Bのように、 2人だけなら、生存率の変化の計算は簡単ですが、人数が増えたり、打ち切りデータも含まれていると大変になって来ます。
カプラン・マイヤー法では、上記のA、Bの例の計算と同様の計算をする方法です。
「生存率が0.5になるまでの時間」、「生存率がほぼ0になるまでの時間」と言ったことが調べられます。
ソフトで簡単に計算できます。
左から右が時間の流れになっていて、生存率がだんだん下がっていく様子がグラフになります。
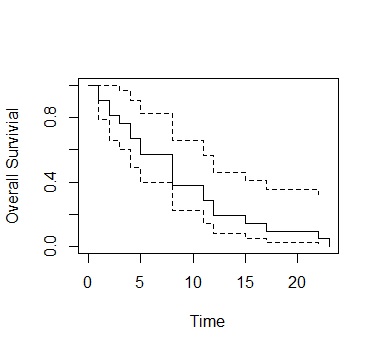
実線が生存率で、点線が信頼区間です。
カプラン・マイヤー法は、生存時間のデータをそのままグラフにする方法になっています。 生存時間のデータは、ヒストグラムや棒グラフで表現することもできますが、 カプラン・マイヤー法を使うと、縦軸を生存率にして、横軸を生存時間にしたグラフで表現できます。
パラメトリックモデルは、生存関数に数式を仮定します。 この点が、カプラン・マイヤー法と異なります。
例えば、
S(t) = exp(-λt)
と仮定すると、
S(0) = 1
S(∞) ≒ 0
となり、指数関数的に、生存率が低くなっていく様子を表現できます。
λの大きさで、実際のデータへの当てはまり方を調整できます。
指数分布を仮定する時は、ハザード関数（H(t))が一定値（λ）の時、つまり、瞬間死亡率に変化がない時です。
ワイブル分布を仮定すると、工業製品の初期の故障のように、瞬間死亡率（故障率）がだんだん低くなっていったり、 使い古した頃の故障のように、瞬間死亡率がだんだん高くなっていくような現象を表せるようになります。 工業製品の寿命を分析する 信頼性工学 という分野では、ワイブル分布が使われます。
ちなみに、ワイブル分布は、 極値統計 の分布でもあります。
医学の分野では、「薬の違いで、生存率に違いはあるか？」ということを調べることが、研究のテーマとして重要です。
例えば、下記のような２種類の変化がある時に、これらを同じものと考えるか、別のものと考えるのか、という分析になります。
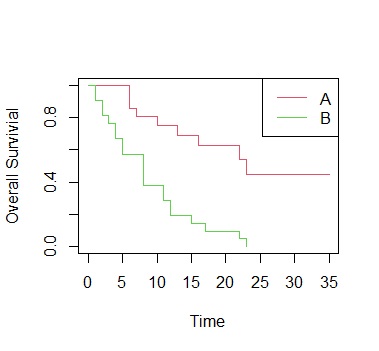
生存率は、だんだん変化する性質のあるものなので、単純に２つの値を比較するような方法が使えません。 そこで、生存率の違いを分析する方法が考案されています。
ログランク検定や一般化ウィルコクソン検定は、 分割表 にデータをまとめて、 独立性の検定 をする方法の発展版です。
時点毎に分割表を作って、統計量を求めます。 その点は、ログランク検定と一般化ウィルコクソン検定は同じです。
一般化ウィルコクソン検定の方は、時点が進むほど、確かなデータが少なくなることを考慮できるようになっていて、 生存率の違いが重視されない計算方法になっています。
コックス回帰分析は、「比例ハザードモデル」とも呼ばれます。 ハザード関数の比が、一定であることを前提にした方法です。
コックス回帰分析は、 ハザード関数は、ノンパラメトリックの部分とパラメトリックの部分の積になっているので、「セミパラメトリックモデル」として分類されます。 時間に依存して変わる部分が、ノンパラメトリックです。 生存率の違いに影響する部分が、パラメトリックになっています。
例えば、生存率の違いに影響する部分は、
exp(a * x)
という式にします。
例えば、xを薬Aの有無で0と1のどちらかを使うようにします。
さらに、生存率の違いに影響する部分は、
exp(a1 * x1 + a2 * x2 +・・・)
という式にすることもできます。
こうすると、生存率の違いの要因が２個以上あっても扱えるようになります。
コックス回帰分析は、 要因が2個以上扱えるのが、ログランク検定や一般化ウィルコクソン検定との違いになっています。 この点が、コックス回帰分析の良いところです。
一般化ウィルコクソン検定では、時間の経過とともに、信頼できるデータが減ることを考慮できます。 この点が、一般化ウィルコクソン検定の良いところです。
コックス回帰分析には、「回帰分析」と入っていますが、 expの中を見ると、確かに 回帰分析 の形になっています。
コックス回帰分析で使う変数は、生存時間、打ち切りか否かがわかる変数、要因の変数の３種類あり、 要因の変数が複数あっても使えるようになっています。
要因の変数が、回帰分析でいうところの説明変数Xになります。
目的変数は、元のデータがそのまま使われるのではなく、生存時間から加工して作られる感じなので、 ロジスティック回帰分析 と似ています。 打ち切りか否かがわかる変数は、この加工の時に補助的な役割で使われます。
Rによる実施例は、 Rによる生存時間分析 にあります。
「Rと生存時間分析（１）」
Rの分析が詳しくのっています。
https://www1.doshisha.ac.jp/~mjin/R/Chap_36/36.html
「ログランク検定と一般化ウィルコクソン検定とは？p値やカプランマイヤー曲線の解釈」
ログランク検定と一般化ウィルコクソン検定のそれぞれと、両者の違いについて、簡単に理解できるような説明になっています。
https://best-biostatistics.com/surviv/logrank.html
「生存時間解析法」
ログランク検定と一般化ウィルコクソン検定の詳しい説明があります。
http://halbau.world.coocan.jp/review/EBNursing4(3)2004.pdf
「入門信頼性 技術者がはじめて学ぶ」 田中健次 著 日科技連出版社 2008
信頼性工学
の本です。確率紙を使ったワイブル解析があり、理論や手順だけでなく、下記のような実務向きの知識も紹介されています。
・寿命データの解析では、ワイブル分布や指数分布が用いられ、修理時間の解析では、対数正規分布が使われている。
・ワイブル解析は、寿命時間のデータに限らず、衝撃試験での印加回数や自動車の走行距離などを横軸にとり、破壊あるいは故障にいたるまでの平均回数や、平均距離などを推定することができる。
・加速試験の妥当性は、形状パラメータが一致するかどうかで判断することができる。
また、尺度パラメータの比で、加速係数を求めることができる。
「【初心者向け】ワイブル分布ってなに？〜高校数学でわかるワイブル分布〜」
ワイブル分布の数式が、どのようにして求められたのかが、わかりやすく書かれています。
https://sts-presents.com/STS01/shikujiri/wible/
「疲労や破壊現象とワイブル分布」
製造業でよく説明される書き方で書かれています。
http://www.mogami.com/notes/weibull.html
「医学統計勉強会 生存時間解析」 宮田 敏 著 2013
説明が丁寧でわかりやすかったです。
https://www.cardio.med.tohoku.ac.jp/2005/news/pdf/20131017_slide.pdf
「Rと生存時間分析（２）」
Rの分析が詳しくのっています。
ワイブル解析もあります。
https://www1.doshisha.ac.jp/~mjin/R/Chap_37/37.html
「生存時間分析の色々なアルゴリズムをまとめてみました」
コックス回帰分析の高度なものも紹介されています。
https://qiita.com/saltcooky/items/409329485be499a5b270
「イベント・ヒストリー分析」 Paul D. Allison 著 福田亘孝 訳 共立出版 2021
離散時間モデル（
ロジスティック回帰分析
）や、コックス回帰分析が紹介されています。
「縦断データの分析 2 イベント生起のモデリング」 Judith D.Singer, John B.Willett 著 菅原ますみ 監訳 朝倉書店 2014
「イベント生起」とは、「薬の効き目が出る」や、「死亡」になります。
イベント生起として、現象を捉える時のポイントについて説明してから、
コックス回帰分析の説明になります。
順路
次は
経時解析
