決定木 の作り方では、「二進木（二分木ともいう）」と言って、枝分かれの枝が必ず２つになっているものが一般的です。 RやPythonで比較的手軽に使えるライブラリは二進木です。
世の中には、N進木（N分木・多進木・多分木）と呼ばれる方法があり、枝が２つ以上の任意の数になります。
筆者の場合、 決定木は、 定量的な仮説の探索 のためのツールとして使うのですが、N進木でないと厳しいです。
まず、決定木の結果に合わせて、現象を２分割の組み合わせで考察しなければいけないのは、とても不便です。 自分は考察できたとしても、決定木を知らない人に同じように理解してもらうのは、とても大変です。
また、二進木の場合は、同じXが複数の層に出て来ることがよくありますが、 こうなってしまうと、木と現象のメカニズムの関連付けが厳しくなります。
「二進木で、内容的にはN進木と同じものを表現できる。」と考えている方もいらっしゃるようです。 数学的・論理的には、そうだとしても、実務的にはとても不便です。
二進木の手法を使うとしても、 人の認知の構造に合わせて、完成した木を再構成する仕組みがあると良いのかもしれません。
CHAIDは、古くからあるN進木の手法です。 ちなみに、筆者が「決定木は役に立つなあ！」と実感したのは、CHAIDを使うようになってからです。
CHAIDは無数の 独立性の検定 （カイ二乗検定）をする仕組みになっています。
そのため、説明変数は質的データを扱います。 説明変数に量的データを使いたい場合は、 １次元クラスタリング をして、質的データに変換すれば使えます。
※ RのCHAIDでは、量的データは自分でコードを書いて変換する必要があります。 IBMのSPSS ModelerにCHAIDが入っていますが、これには量的データを質的データに自動的に変換する機能が含まれているようです。
CHAIDの特徴として、明らかな違いがあってもN数が少ないと枝分かれしない点があります。 この特徴は、無闇に枝が細かくならないようにしてくれるので便利です。
J48とC4.5は同じもののようです。 C5.0は、C4.5の発展版のようですが、使ってみて違いらしい違いは見当たりませんでした。
説明変数は、量的・質的どちらがあっても使えます。 質的データはN進木になり、量的データは二進木になるので、量的データにもN進木を期待している場合は適さないのですが、 CHAIDと違って量的データに前処理がいらないのは便利です。
RによるCHAIDとC5.0の実施例は、 RによるN進木 のページにあります。
J48は、Wekaで使える手法のひとつです。 RではRWekaを使うとできるようですが、RWekaはインストールでJAVAの設定が必要になります。 Rで実行することが必須ではないのなら、Wekaの方が簡単なので良いと思います。
左が、CHAIDの「XやYに量的データが混ざっている場合」で作ったデータの結果です。量的データのX1が選ばれ、2進木にはなりました。
右が
Wekaにある「wether.numeric」というサンプルデータの結果です。
N進木になりました。
RapidMinerには、「Decision Tree」という名前の手法が入っているのですが、 質的データはN進木になり、量的データは二進木になるので、C4.5と同じか、C4.5に近いアルゴリズムを採用しているようです。
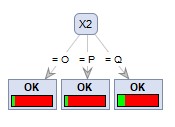
左が、CHAIDの「XやYに量的データが混ざっている場合」で作ったデータの結果です。
デフォルトの設定では枝分かれが起きず、「minimal gain」0.01というパラメータをデフォルトの10分の1の数値にしたら枝分かれしました。
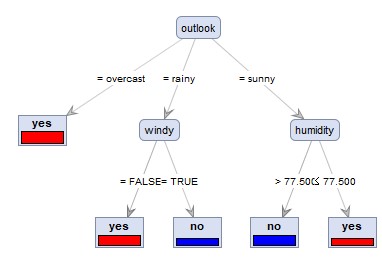
右が
Wekaにある「wether.numeric」というサンプルデータをcsv形式にして、Yの列名を変えたものの結果です。
いずれも、N進木になりました。
R-EDA1では、C5.0ができます。
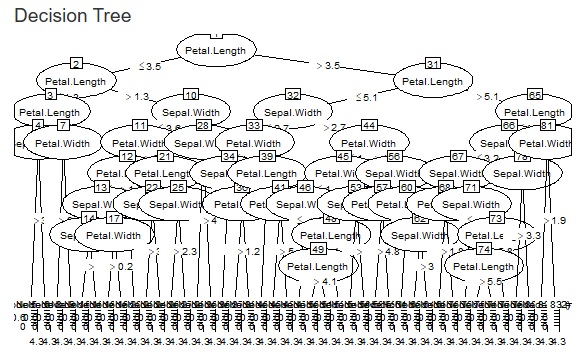
決定木を作る時の木の細かさは、デフォルトにお任せにしていたのですが、巨大な木（枝分かれが細かい木）になることがあります。 因果関係の分析では、３番目くらいまでの枝分かれがどうなるのかが重要で、巨大な木は不要なことが多いです。 また、巨大な木をOKにすると、計算時間が非常に長いことがあります。 さらに、巨大な木は、過学習とも言えることがあり、ロバストではないので使いにくいです。
そこで、枝分かれ先の最小の大きさを設定できるようにしました。
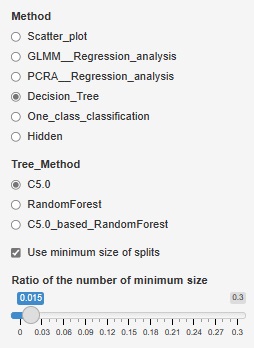
「Use minimum size of splits」にチェックを入れると、設定できるようになります。
チェックを外すと、デフォルトにお任せになります。
例えば、「Ratio of the number of minimum size」を「0.1」にすると、最小になる枝分かれは、全体の0.1になります。
1000行のデータでしたら、100よりも小さくはならなくなります。
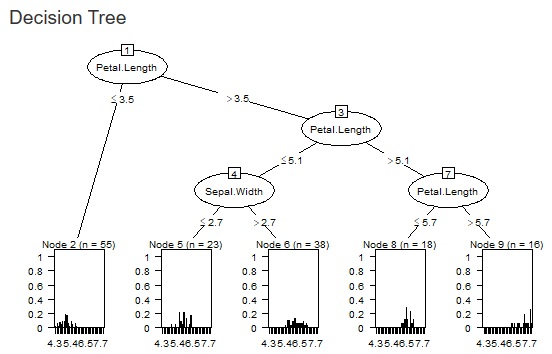
下の２つの図は、同じデータに対して、設定値を変えた場合の例です。
同志社大学 金明哲先生のページ
WekaのJ48の使い方
https://www1.doshisha.ac.jp/~mjin/R/Chap_20/20.html
順路
次は
ランダムフォレスト
