トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

ROC曲線とAUC

ROC曲線（Receiver Operating Characteristics Curve）やAUC（Area Under the receiver operating characteristics curve）は、 混同行列 を使って、 パターン認識 の結果を評価するための方法です。

「まず、本当は陽性の人を、陽性として判定する割合はできるだけ大きくしたい。 しかし、本当は陰性の人を、陽性と判定する割合はできるだけ小さくしたい」、という意識がある時に使われます。

判定値と、FP率・TP率の関係

FP率とTP率は、偽陽性率と真陽性率のことで、
FP = (FP + TN)
TP = (TP + FN)
で定義されます。

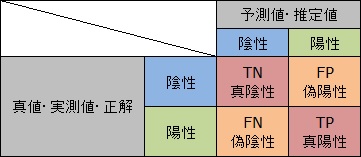
FP率は、本当は陰性なのに陽性と判定された人の割合で、TP率は、本当は陽性で陽性と判定された人の割合です。 陽性と判定された人の中で、正しく判定された人と、間違って判定された人を分け、それぞれを違う母数で割っています。

冒頭の話を定量的に扱う時に使います。 ベストな状況とは、TP率が一番大きい中で、FP率ができるだけ小さい時になります。

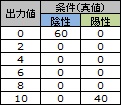
FP率とTP率を、判定値が３と７の時の混同行列について計算してみます。

判定値が3の時は、本当は陽性の人を陰性と判定することは絶対なく、この時のTP率は1になっています。

判定値が7の時は、本当は陰性の人を陽性と判定することは絶対なく、この時のFP率は0になっています。

TP率とFP率の見方ですが、 絶対に間違わない判定方法が可能であれば、その方法ではTP率が1とFP率が0が両立させられることがわかります。

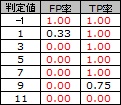
上記では、判定値の例は２つだけでしたが、判定値を少しずつ変えると、下図のようになります。

FP率とTP率を計算する目的

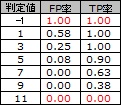
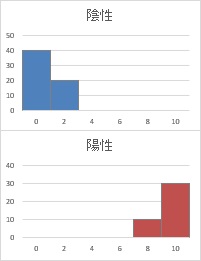
TP率が一番大きい中で、FP率ができるだけ小さい時は、判定値が3である時でした。 判定値が3の時をヒストグラムに追記してみると、 どういう判定をしているのかがわかりやすいと思います。

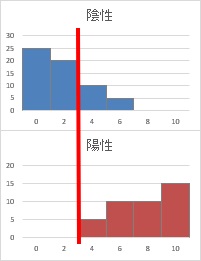
このページの例のように、わざわざFP率とTP率を計算しなくても、ヒストグラムを見るだけで、判定値を3にすることがベストであることを見つけられることもあります。

FP率とTP率の計算が重要になるのは、もっと複雑なグラフから判定値を決める必要がある場合や、 複数の測定方法や計算式を比較する場合です。

ROC曲線

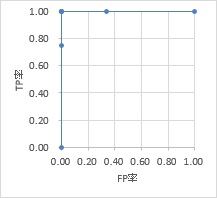
FP率とTP率の散布図は、ROC曲線と呼ばれています。 上記のFP率とTP率の場合は、下図になります。

完璧な判定ができる場合のROC曲線

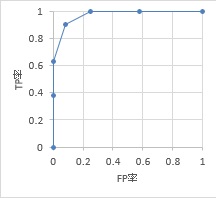
完璧な判定ができる場合のデータとROC曲線は、例えば下のような場合です。 左上の角で、直角に折れ曲がる線になっています。

複数の測定方法や計算式を比較したい時は、 直角に折れ曲がる線に近いほど、良い方法と言えます。

AUC

上の２つのROC曲線を見ると、完璧な判定ができる場合は、ROC曲線の下側に、 縦軸が0から1、横軸が0から1の範囲の全部が入りますので、この面積は1です。

完璧から離れるほど、面積が狭くなりますので、この面積は判定の能力の指標になります。 この面積は、AUCと呼ばれています。 AUCを使うと、ROC曲線の比較を「見た目」ではなく、定量的に行うことができます。

AUCは、0から1の間にあります。 0.5ちょうどが、パターン認識がデタラメの場合です。

上の例では、陽性であれば、出力値が高くなっていましたが、実際には逆の場合もあります。 逆の場合は、AUCが0から0.5の間になります。

ROC曲線やAUCの信頼区間

ROCやAUCは、割合から求まりますので、サンプル数の情報が消えています。 推定 を知っていると、サンプル数を考慮して、ROCやAUCの確からしさを評価したくなります。

書籍でそこまで書かれているものはないようなのですが、 ネット上では、Rなどでそこまで評価できるプログラムが紹介されているようです。

参考文献

「ITエンジニアのための機械学習理論入門」　 中井悦司　著　技術評論社　2015
ロジスティック回帰分析 の解説の中で、ROC曲線が出て来ます。 ロジスティック回帰分析では確率を出せますが、この確率の数字では、精密検査を受けさせるかどうかの医師の判断には向かないとしています。
偽陽性率（FP率）= FP / (TN + FP)　本当は陰性の人（分母）を、「陽性」と判定してしまう割合
真陽性率（TP率）= TP / (TP + FN)　本当は陽性の人（分母）を、「陽性」と判定できる割合
としています。 医師としては、真陽性率をできるだけ高くして、偽陽性率をできるだけ低くしたいと思うので、 その判断にROC曲線による評価が合っています。

「Pythonではじめる機械学習　scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎」　Andreas C.Muller, Sarah Guido 著　オライリー・ジャパン　2017
モデルの評価の方法として、 ROC曲線やAUCが解説されています。 Pythonを使う時のコード付きです。

「フリーソフトではじめる機械学習入門」 荒木雅弘　著　森北出版　2014
ROCやAUR（＝AUC）の考え方がコンパクトにまとまっています。 Weka での実施例があります。

「データサイエンス講義」　Rachel Schutt、Cathy O’Neil 著　瀬戸山雅人　他　訳　オライリー・ジャパン　2014
AUCが1に非常に近い時は、「モデルが良い」と考えたくなりますが、実際のデータ分析では「データの因果関係が間違っている」と考えた方が良いそうです。 この本では、このような現象を「データのリーク」と呼んでいます。

順路 次は 偽陽性と偽陰性のバランス