トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
重回帰分析 のページの説明で、 「無関係の変数をモデルに加えても、決定係数（寄与率）には大きくなる性質があるため、単純に大きければ良いと言う尺度ではありません。」と説明しています。 また、 説明変数が２つのモデルの推定 のページでは、この知識を使って、寄与率が少し大きくなるだけの変数は、モデルに加えないようにガイドが作られています。
寄与率 のページでも説明していますが、一般的な重回帰分析で扱うデータの場合、 モデル式に入っている個別の因子の寄与率を調べることはできないことを説明しています。 （ 個別の因子の寄与率 のページで説明しているように、条件を満たしていれば、調べられます）
個別の因子の寄与率は調べられないのですが、「この変数を加えたら、寄与率はいくつ増えるか？」という事は調べられます。
このページでは、「無関係の変数を加えた場合、寄与率はどのくらい増えるのか？」ということを筆者が調べた結果を説明します。
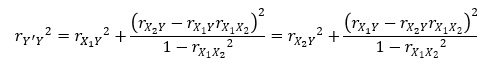
上の式は、目的変数が１つ、説明変数が２つの場合の寄与率を、相関係数で表した式です。
変数が３つあるので、相関係数は３個ありますが、それらを使う式になっています。
単回帰分析の寄与率に、追加する形の式になっています。
この追加した部分は、必ず０以上になります。 ０になるのは、特殊な場合です。
つまり、説明変数として適切かどうかに関わらず、変数が増えると、決定係数が増える式になっています。
X1という変数があり、X1の単回帰式の形でYが決まっている場合を想定します。 そこに、X2という変数を加えた場合の、寄与率の増加量を調べます。
手順としては、まず、X1を乱数で発生させます。 次に、X1に乱数を加えて、Yを作ります。 乱数のばらつき方を変えることで、YとX1の相関の大きさを変えます。
X2は、X1と独立に乱数で作った場合と、X1に乱数を加えて、X1と相関が強い場合を作ります。
サンプル数nは、10、100、1000の３通りにします。
パターン事に100個データを作成して、その都度、寄与率の増加量を計算します。
寄与率の増加量は、下の式の赤枠の中に相当します。
増加量だけでなく、この式に入っている相関係数との関係も見ることにします。
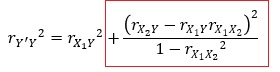
サンプル数には、大きく依存する結果になりました。 X1とX2の相関と、X1とYの相関の依存性も調べましたが、特に気にしなくて良いことがわかりました。
横軸を、X1とX2の相関係数にして、縦軸を寄与率の増加量にしたグラフです。
サンプル数ごとに、グラフは分け、縦軸の範囲を変えています。
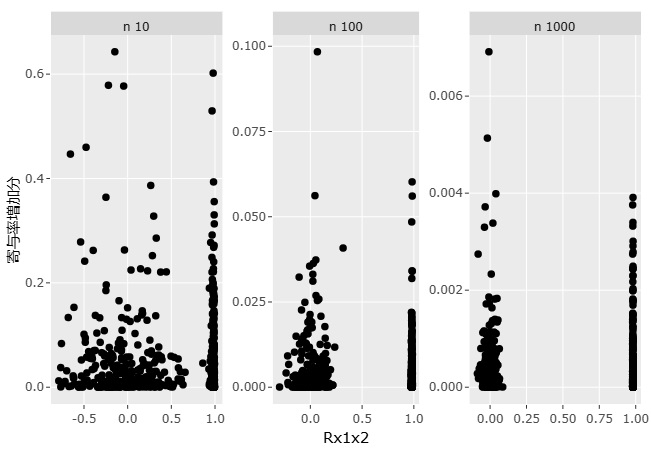
X1とX2の相関の大きさは、影響していないことがわかります。
横軸を、X1とYの相関係数にして、縦軸を寄与率の増加量にしたグラフです。
サンプル数ごとに、グラフは分け、縦軸の範囲を変えています。
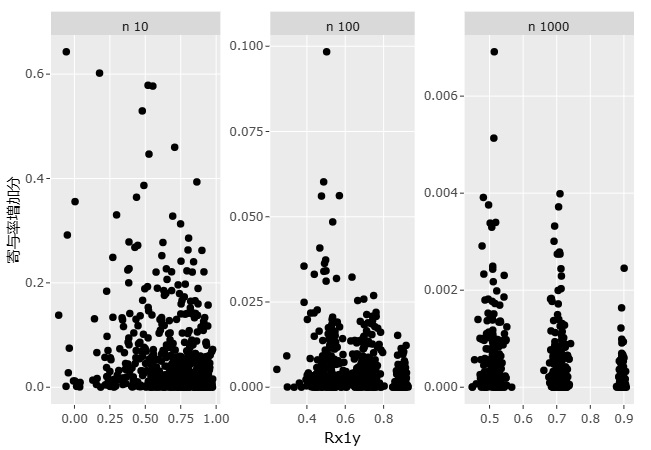
サンプル数が10の時は、X1とYの相関は関係なさそうですが、サンプル数が100と1000の時は、相関が弱いほど、増加量が大きくなっているように見えます。
上のグラフは、縦軸の範囲を変えていますが、縦軸の範囲を変える必要があるほど、サンプル数の影響が大きいです。
縦軸の範囲を合わせると、下のグラフになります。
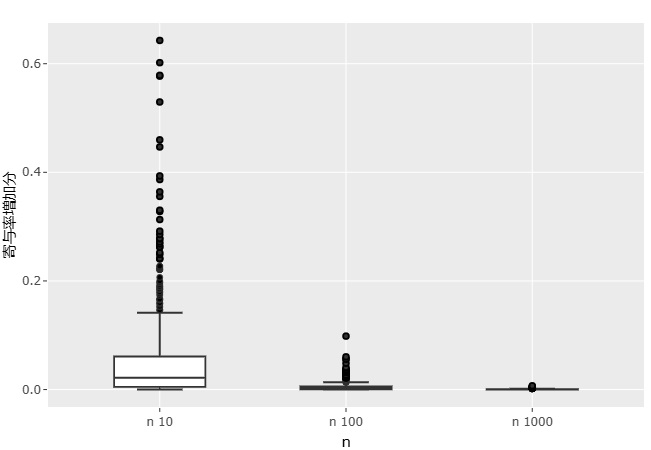
他の要因は考えず、サンプル数の違いだけでグラフを作り、サンプル数ごとに縦軸の範囲を変えると、下のグラフになります。
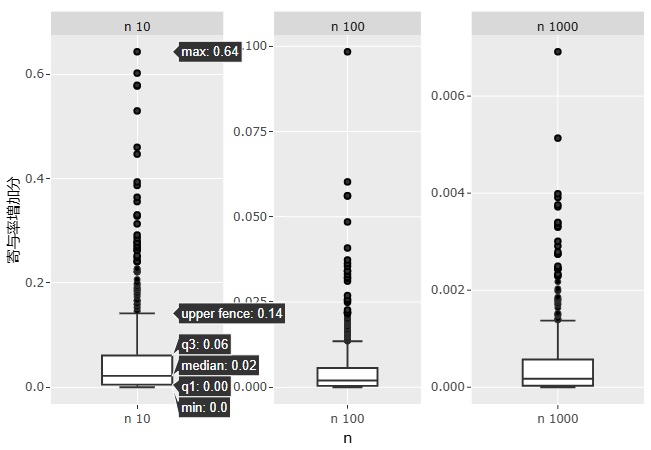
サンプル数が10個の時は、上側のひげ（upper fence）が0.14です。 このサンプル数の時は、0.14くらいの増加量でも、珍しくないことになります。 外れ値として、0.14よりも上は、0.6（60%）くらいの時もあります。 目安としては、「0.2よりも大きければ、X2も説明変数にした方が良いかもしれない」と言えそうですが、0.2よりも大きくても、グラフを丁寧に確認する必要がありそうです。
サンプル数が100個の時は、外れ値を含めたとしても、「増加量が0.1よりも大きければ、X2を説明変数にした方が良さそう」と言えます。
サンプル数が1000個の時は、外れ値を含めたとしても、「増加量が0.01よりも大きければ、X2を説明変数にした方が良さそう」と言えます。
「パラドックスで学ぶ統計学」 岩崎学・川崎玉恵 著 共立出版 2025
２変数の重回帰分析と、単回帰分析について、決定係数の関係式を紹介しています。
この本の抑制についての章では、変数を追加することで、決定係数が0.09から0.12に増えたことに対して、「追加した変数が現象に影響があることを示す」という解釈をしています。
この本にはサンプル数が書かれていないのですが、上の結果から考えると、サンプル数が100個程度なら、変数を追加することには意味がなく、1000個程度なら、意味があると考えられます。
順路
次は
パス解析
