コピュラの理論が必要となる典型的な例が、上の図のようなデータです。 このデータでは、XとYのそれぞれが、正規分布をしています。
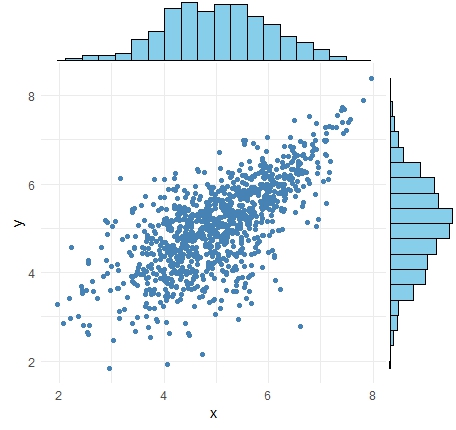
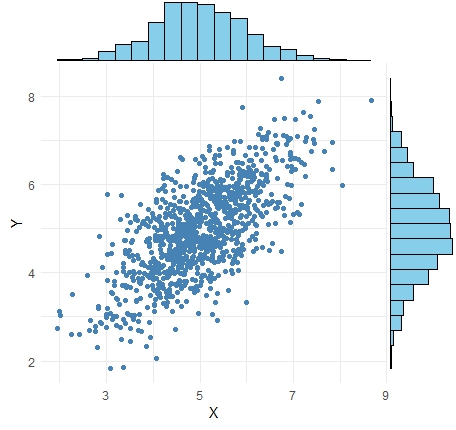
コピュラの理論が必要となる典型的な例が、上の図のようなデータです。
このデータでは、XとYのそれぞれが、正規分布をしています。
一見すると、「XとYは、相関が強そう」という感じのデータになっています。 実際、 相関係数 が0.7なので、そこそこ強いです。
ところが、よく見ると、相関はXとYが大きい領域の時に強く、XとYが小さい領域は弱いように見えます。
このデータが時系列データの場合、このグラフの意味するところは、「普段相関がないように見える変数同士でも、普段とは異なる値の時は、強く相関することがある」や、その逆です。
コピュラについての文献を探すと、金融業界のものばかり見つかります。 金融業界では、「領域によって相関の強さが違う」という性質を考慮しなかったために、過去に大失敗があったそうです。
ここでは、コピュラの数学的な視点ではなく、データの見方としての視点で説明します。
「コピュラ」は、不思議な響きの言葉です。 もともとラテン語の「つなぎ合わせる」が語源とのことです。
このページは、統計学の話として、コピュラを説明していますが、 「コピュラ」は、まったく違う意味で言語学でも出てきます。 言語学の方は、主語と述語をつなぐ品詞のことです。
このサイトには、 言語学 のページもあります。 筆者は、言語学の方でも「コピュラ」という言葉を見たことがあったので、最初、統計学のコピュラと混乱しました。
上のグラフは、それぞれの変数だけをヒスグラムで表し、両方が一度に見るために散布図で表しています。
それぞれの変数だけを見ると、正規分布ですが、これを「周辺分布」と言います。
両方を一度に表しているのが、「同時分布」と言います。
コピュラは、周辺分布と同時分布を関係付ける関数のことです。
コピュラだけを見ると、下のグラフになります。
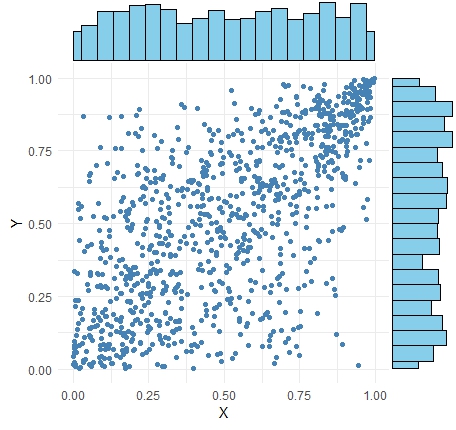
XとYは、いずれも０から１までの値になる一様乱数になっています。 １に近いあたりには、プロットが偏っていますが、０に近いあたりはばらついています。
このコピュラについて、周辺分布がを正規分布になっているものが、冒頭のグラフに近いものになります。 このコピュラは、「ガンベルコピュラ」と言います。
下のコピュラは、「ガウシアンコピュラ」と呼ばれています。相関係数が0.7になります。
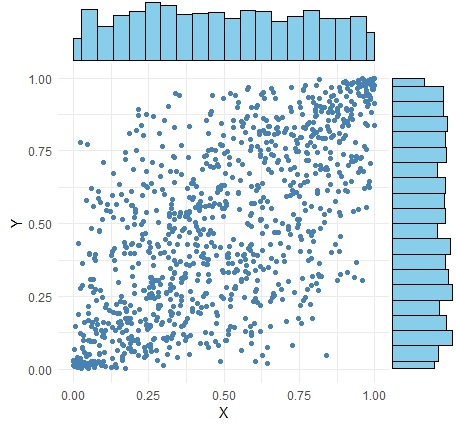
ガンベルコピュラと違って、１に近い方と、０に近い方の両方で、プロットが偏っています。
ガウシアンコピュラで、周辺分布が正規分布だと、二次元正規分布になります。
下の例は、クレイトンコピュラです。
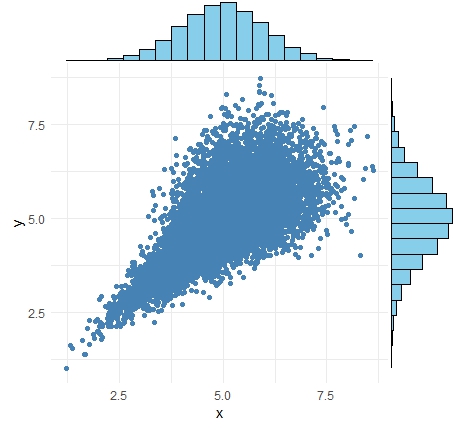
クレイトンコピュラは、Xが大きければ大きいほど、Y方向のばらつきが大きいです。 この見方をすると、 比例分散 と区別がつきにくいです。
上のグラフは、下のRのコードを使って作りました。
library(copula)
library(ggplot2)
library(ggExtra)
# パラメータ設定
n <- 1000 # サンプル数
theta <- 2 # パラメータ（正の値）
# コピュラを定義
cop <- claytonCopula(param = theta, dim = 2) # クレイトンコピュラ
#cop <- gumbelCopula(param = theta, dim = 2) # ガンベルコピュラ
#cop <- frankCopula(param = theta, dim = 2) # フランクコピュラ
#cop <- amhCopula(param = theta, dim = 2) # amhコピュラ
#cop <- joeCopula(param = theta, dim = 2) # ジョーコピュラ
#cop <- normalCopula(param = 0.7, dim = 2) # ガウシアンコピュラ(相関係数が0.7)
# コピュラから一様分布データを生成
u <- rCopula(n, cop)
# 各変数を標準正規分布に変換。（ただし、全部正の値にするので、５をプラスする）
x <- qnorm(u[, 1])+5
y <- qnorm(u[, 2])+5
df <- data.frame(X = x, Y = y)
# プロットして確認
p <- ggplot(df, aes(x = x, y = y)) +
geom_point(color = "steelblue") +
theme_minimal()
ggMarginal(p, type = "histogram", fill = "skyblue", bins = 20)
thetaの範囲ですが、
クレイトンコピュラは、０以上です。
ガンベルコピュラとジョーコピュラは、１以上です。
フランクコピュラは、無限大と無限小の範囲です。
amhコピュラの、-1から1の間です。
「コピュラ理論の基礎」 江村剛志 著 コロナ社 2025
応用ではなく、数学的な話題を中心にして書かれています。
「損害保険数理」 岩沢宏和・黒田耕嗣 著 日本評論社 2015
「ファイナンスとデータ解析」 日本金融・証券計量・工学学会 編集 朝倉書店 2015
「クレジットリスク 評価・計測・管理」 D.Duffie, K.J.Singleton 著 共立出版 2009
「ベイズ統計学とファイナンス」 津田博史・ 中妻照雄・ 山田雄二 編 朝倉書店 2009
「フィナンシャルリスクマネジメント」 ジョン・C.ハル 著 ピアソン・エデュケーション 2008
「金融リスクとコピュラ」 吉羽要直 著 日本銀行金融研究所 2009
https://ibisml.org/ibis2009/pdf-invited/yoshiba1.pdf
ネット上の記事で、一番わかりやすかったです。
「コピュラの金融実務での具体的な活用方法の解説」 戸坂凡展・吉羽要直 著 日本銀行金融研究所 2005
https://www.imes.boj.or.jp/research/papers/japanese/05-J-19.pdf
計算が詳しいです。
順路
次は
単回帰分析
