トップページ |
統計学の解釈学 |
このサイトについて
トップページ |
統計学の解釈学 |
このサイトについて
以下は、筆者の私見です。 誤解があれば、ご教示いただけると幸いです。
ARモデルの係数の決まり方 のページでは、ARモデルの係数と、三角関数の周期には関係があることを示しています。
このページの結果から、上記の知見を導いています。
なお、三角関数以外も含む、周期的なデータ全般と、ARモデルの関係については、 周期性とARモデルの関係 のページがあります。
以下の三角関数のデータついて、AR(1)、AR(2)、AR(3)を確認します。
周期が６の場合は以下になります。
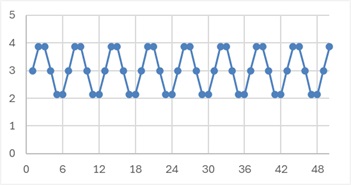
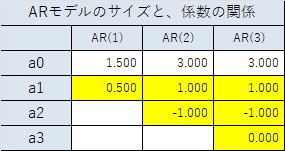
周期が12の場合は以下になります。
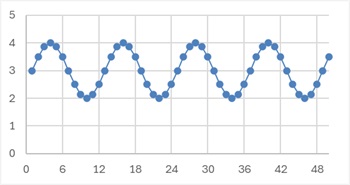
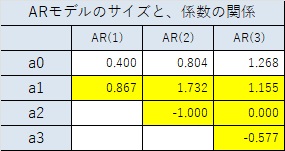
周期が24の場合は以下になります。
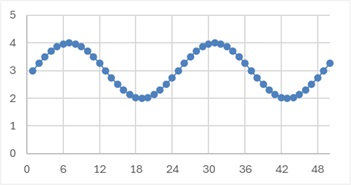
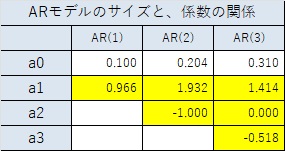
周期が480の場合は以下になります。
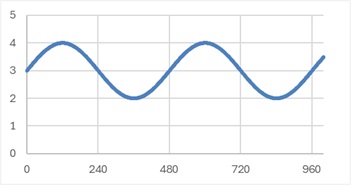
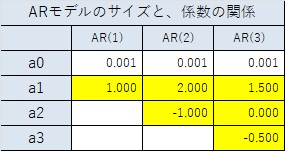
上記の結果から、周期が大きくなるほど、係数が ２次式 のARモデルに近付いていることがわかります。
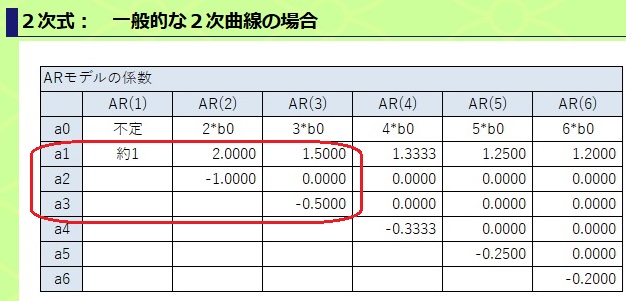
上記の結果から、ひとつの仮説ができます。 それは、以下のものです。
この仮説について、周期を変えて調べた結果が以下になります。
仮説が正しいことはわかりました。
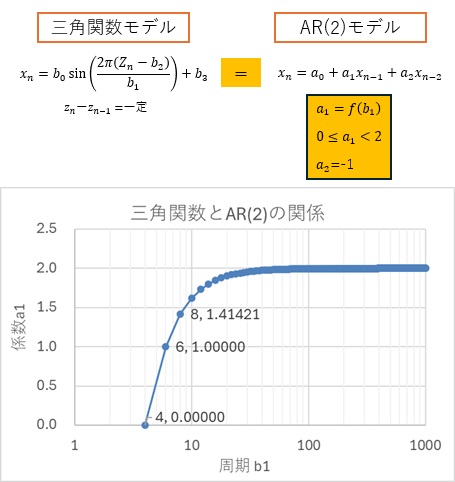
この結果は、振幅や位相を示す、b0、b2、b3については示していませんが、筆者が試した範囲では、 a1、a2に対して、これらは無関係でした。
上記は、２次式のAR(2)で出て来る「a1 = 2、a2 = -1」という係数に関係するものでした。
これと似たもので、
３次式のAR(3)
には、以下の決まり方があります。
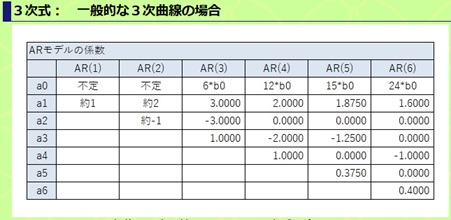
経験的にですが、筆者は、３次式のAR(3)で出て来る「a1 = 3、a2 = -3、a3 = 1」という係数に近い値でモデルを作ると、周期的なデータができることを知っていました。
例えば、下記のようになります。
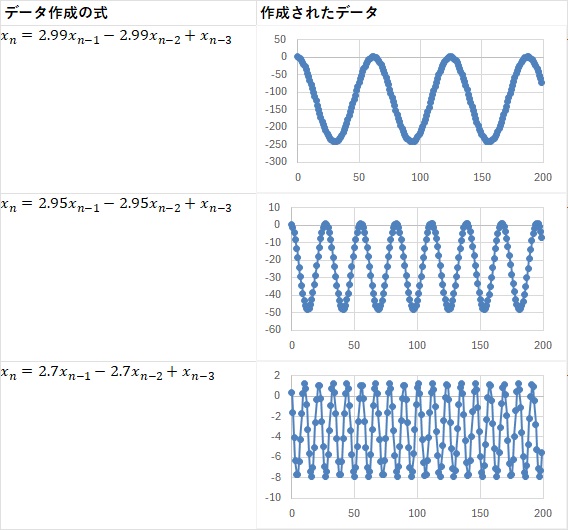
AR(2)との関係の時は、三角関数として作ったデータから、ARモデルを作って、AR(2)の係数を求めました。
３次式のAR(3)として作ったデータから、ARモデルを作ると、２次式のARの時の、「a1 = 2、a2 = -1」に近い値が求まります。
しかも、３次式の係数の時よりも、１引かれた値が求まることが経験的にわかっています。
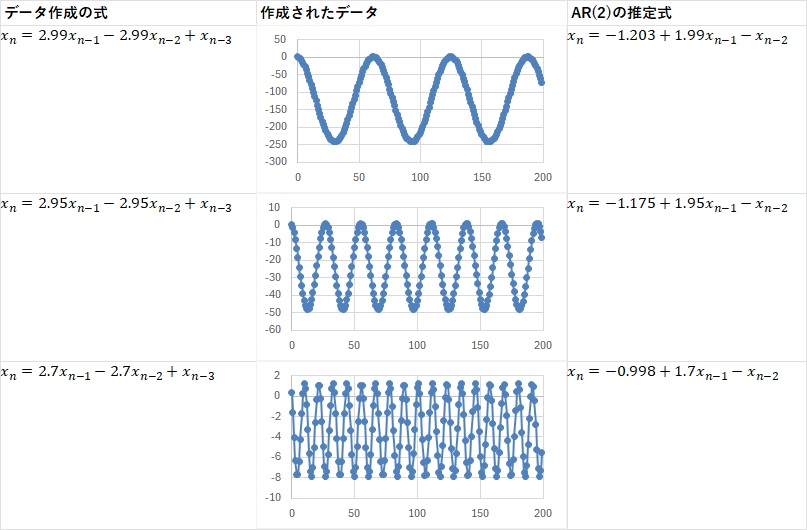
以上をまとめると、下記になります。
