トップページ |
統計学の解釈学 |
このサイトについて
トップページ |
統計学の解釈学 |
このサイトについて
以下は、筆者の私見です。 誤解があれば、ご教示いただけると幸いです。
ARモデルの係数の決まり方 のページでは、ARモデルの係数からは、周期性が読み取れないことを説明しています。
このページの結果から、上記の知見を導いています。
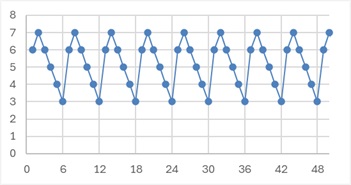
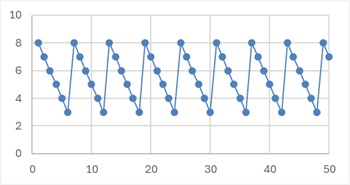
上のグラフは、１周期が６個のサンプルになっています。
なお、このページのデータはどれも約1000個のセットですが、グラフは見やすくするために最初の50個で作っています。
以下は、上記の結果について、他の次数の場合や、他の項数の場合についても確認したものです。 結果は、同じです。
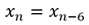
上記の場合のARモデルは、上の式で表せます。
この式は、直接的には、６個前のサンプルと、値が同じであることを表しています。
上のグラフは、ノコギリの歯のようなデータですが、１周期が６のデータなら、式は同じになります。
上の式にある「Xn-6」というのは、元のデータを６行ずらしたデータです。 そこで、Xn-6という変数を作って、回帰分析をすると、以下の結果になります。
Xn-6という変数１個だけで、重相関Rが1なのは、Xn-6だけで、Xnを完全に予測できることを表します。
また、その時の係数が「1」と出ているので、上の式は、この分析からも正しいことがわかります。
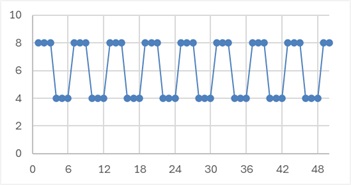
上のデータも、１周期が６個になっているので、下の式で表せます。
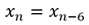
このデータは、少し特殊です。 真ん中に軸があって、半周期前は、その軸に対して、鏡に映したように対称的なデータになっています。 ここでは、「振動データ」と呼ぶことにします。
３行ずらした変数を作って回帰分析をすると、以下のようになります。
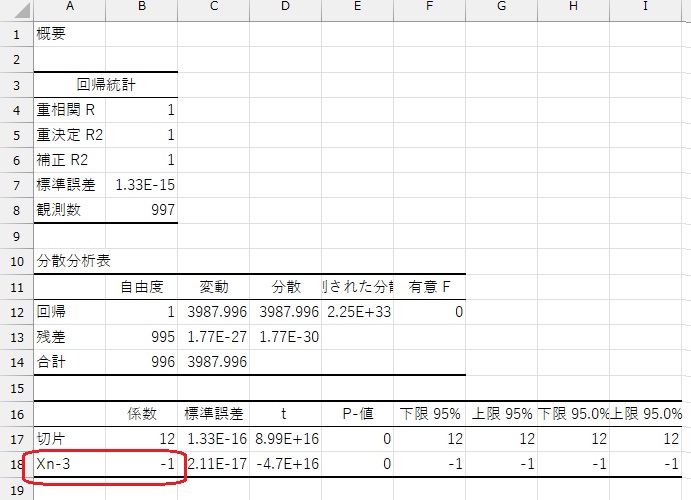
この分析結果から、以下のARモデルが導けます。
「12」と言う数字は、軸が「6」の位置にあって、その２倍であるところから決まっています。
「12」が軸を表して、「-1」が対称性を表しています。
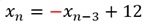
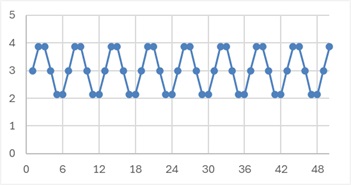
以下は、周期が３の振動データの、別の例です。
式の中で、軸が3の高さになることで、上の式で「12」となっていたところが「6」になっていますが、
Xn-3の係数が「-1」になる点は同じです。
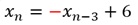
上記では、「１周期前の項だけ」や「半周期前の項だけ」のモデルでした。
ここではフルモデルを考えます。
フルモデルというのは、例えば、上記のようにXn-6を含めたいのなら、フルモデルは、以下になります。
Xn-5までの項も、すべて入れます。
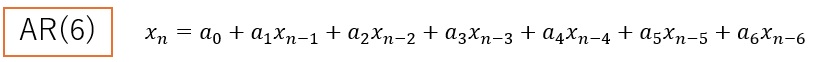
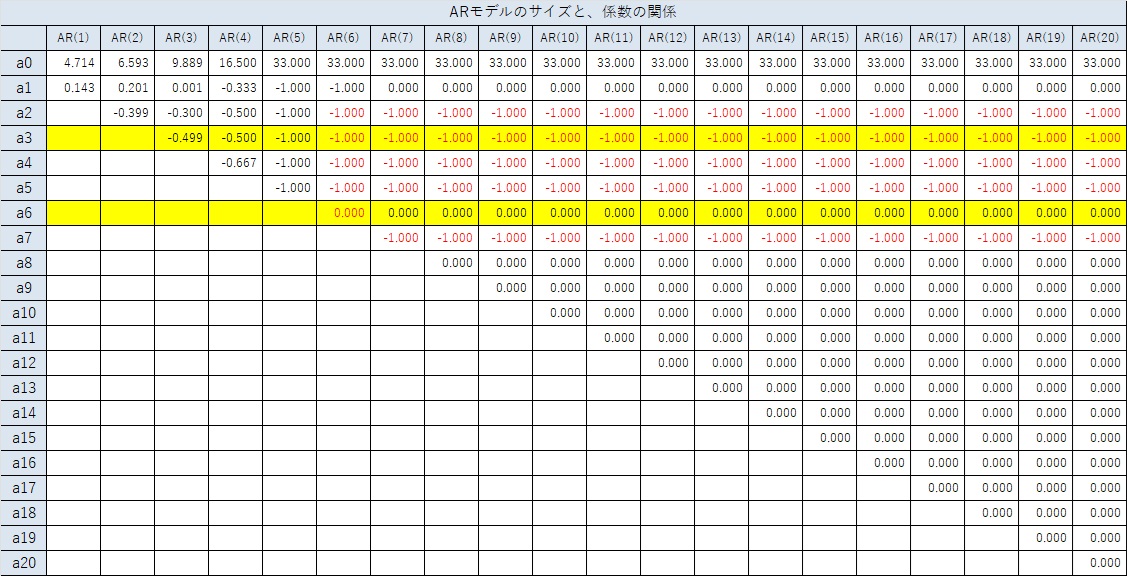
下記は、AR(1)から、AR(20)までのフルモデルについて、データと係数の関係を示しています。
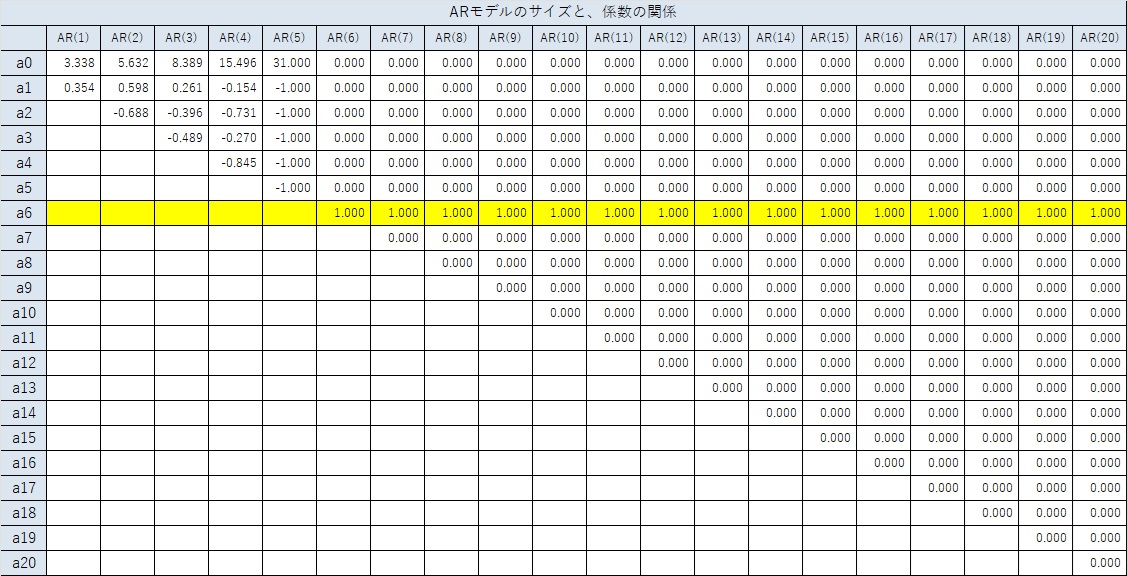
AR(1)からAR(5)までは、１周期前の項がないので、複雑な予測式になっています。
AR(6)以上になると、a6の係数が１で、他は０になっています。つまり、以下の式が求まっています。
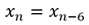
振動データの場合は、以下のようになります。
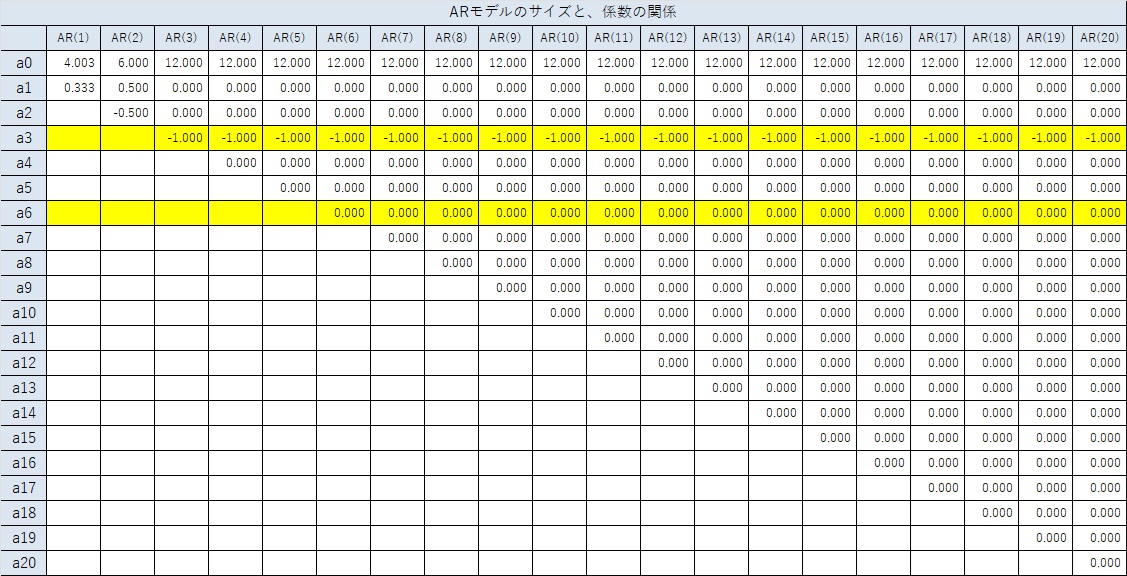
この分析結果から、以下のAR(3)以上では、ARモデルが導けます。
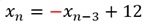
周期が６ですが、以下のモデルは求まりません。
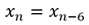
上記では、１周期前の項だけと、フルモデルを説明して、項の数が十分にあれば、両者が一致することを説明しました。 また、振動データの場合は、半周期前の項だけのモデルと、フルモデルが一致する例を説明しました。
これらの一致は、当たり前のように見えるかもしれませんが、一致しない事は、よくあります。 そのため、「ARモデルの係数からは、周期性が読み取れない」というのが、このページの結論です。
以下で、一致しない例を説明します。
冒頭の例と、少し違う例です。
フルモデルは、多くの項に「-1」が入る形になっています。
上記の振動データの例の、２つ目の例の場合は、以下のようになります。
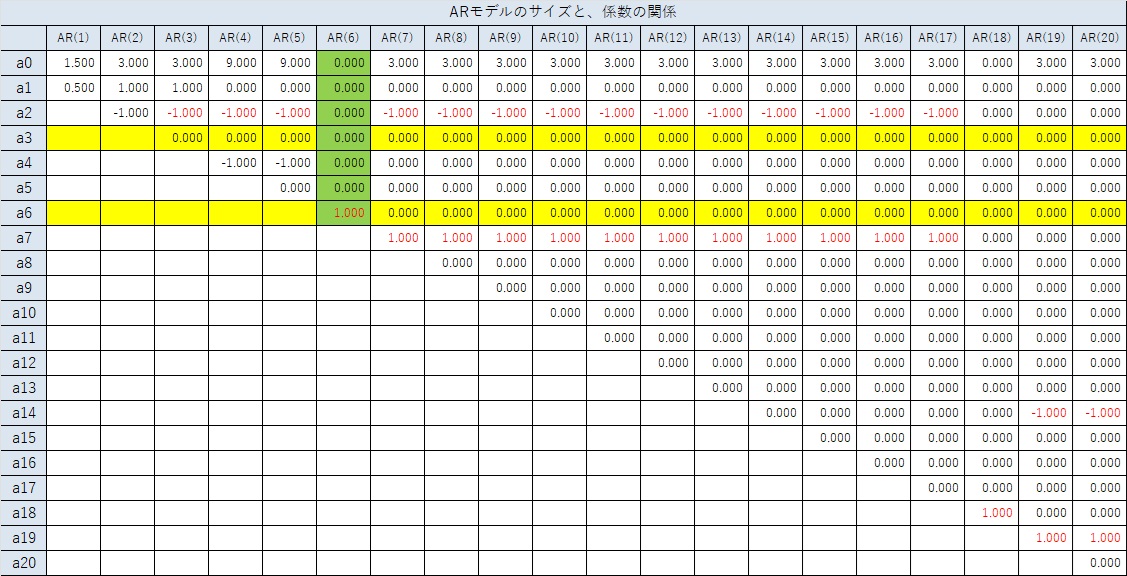
AR(6)の時に、Xn-6の項だけのモデルに相当する係数が求まっています。
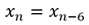
AR(6)以外では、Xn-3の係数になるa3や、Xn-6の係数になるa6が0になっていて、他の項に1や-1という数字が入っています。
ここまでは、周期があった時に、その周期や、半周期の項数のARモデルに注目しています。 そのため、AR(1)、AR(2)、AR(3)については、触れていませんでしたが、ここからはAR(1)、AR(2)、AR(3)に注目します。
まず、以下の振動データの時について、AR(1)、AR(2)、AR(3)を確認します。
上記の振動データは、周期が６でした、
周期が12の場合は以下になります。
周期が24の場合は以下になります。
周期が480の場合は以下になります。
上記の結果から、周期が大きくなるほど、係数が以下に近付いていることがわかります。
振動データの場合、半周期前の項に「-1」をかけることでもモデルが作れました。
一方、このページでは、振動データではない場合や、半周期前の項ではないところでも、係数に「-1」が出て来ることがわかります。
そのため、フルモデルを作った時に、負の値の係数や、「-1」という係数が表れるとしても、「振動を起こす項だ」ということにはなりません。
フルモデルの係数は、セットで使われることに意味があり、単独で何かの解釈には使えないのですが、単独で解釈している文献を見かけたことがあります。
