トップページ |
統計学の解釈学 |
このサイトについて
トップページ |
統計学の解釈学 |
このサイトについて
以下は、筆者の私見です。 誤解があれば、ご教示いただけると幸いです。
ARモデルの係数の決まり方 のページでは、ARモデルの係数の決まり方について、全体的なまとめを書いています。
このページは、それらの内、多項式とARモデルの係数の関係について、筆者が調べたことを記録したものです。
具体的には、以下の式について、係数bのグループがいろいろ変わっても、係数aのグループはいくつかのパターンに決まっていることを調べます。
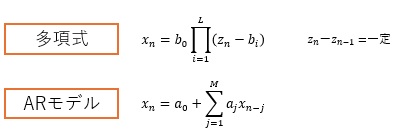
例えば、「２次式に近い３次式」のような場合は、この限りではないのですが、
典型的な多項式の曲線の場合は、以下のようにARモデルの係数が決まるというのが、このページの結論です。
以下では、１次式から順に、検証します。
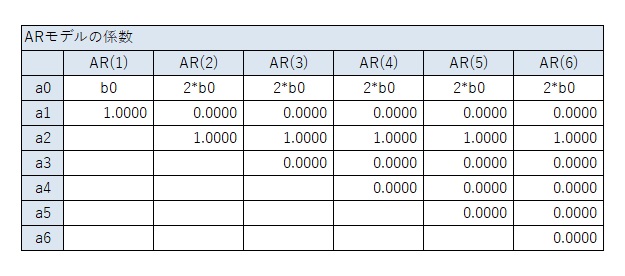
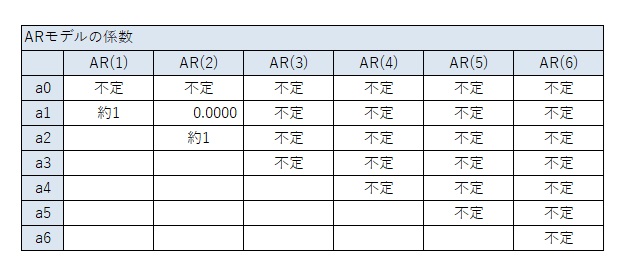
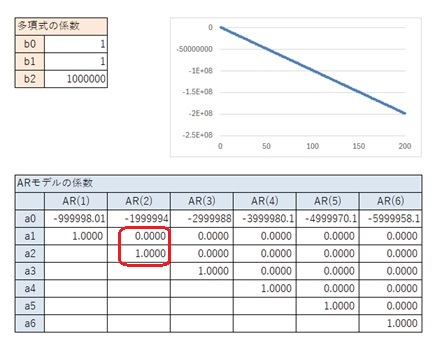
以下の結果から、１次式の場合は、上の表が結論です。
なお、「a0の値 = b0が1の時の値 * b0」という関係になるのは、式の形からわかることなので、２次式以上では検証は省略します。
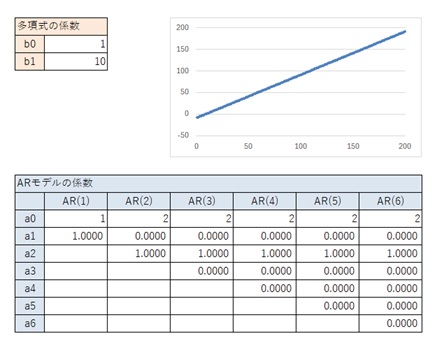
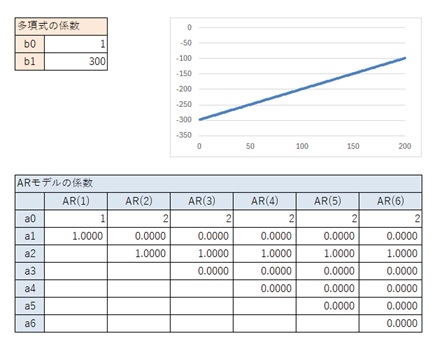
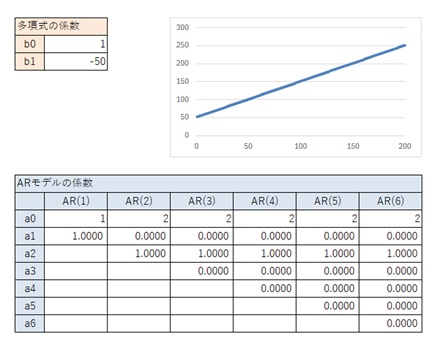
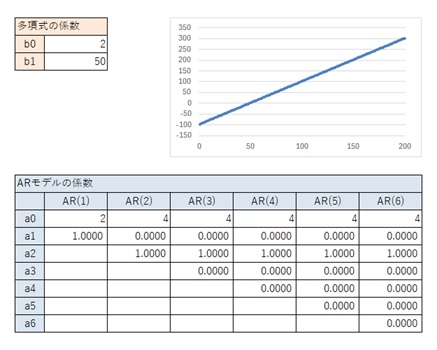
２次式以上では、場合分けをします。
以下の結果から、一般的な２次曲線の場合は、上の表が結論です。
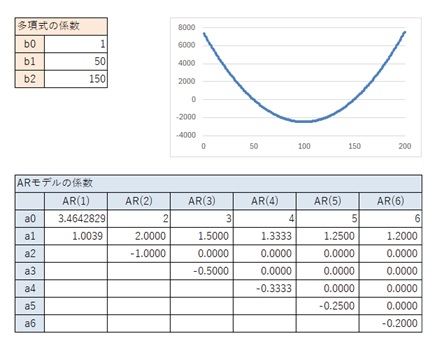
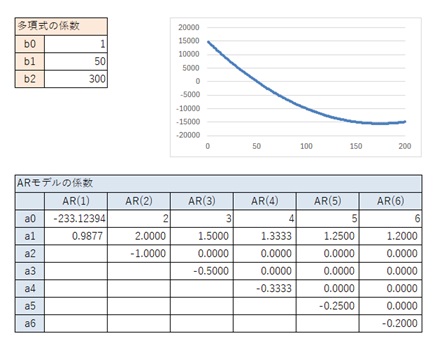
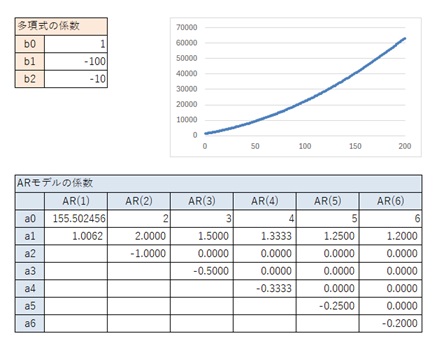
以下の結果から、一般的な２字曲線の場合は、上の表が結論です。
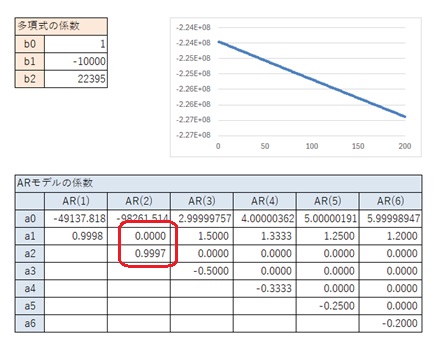
２次式だとしても、データの範囲では１次式に近い場合、AR(2)の時のパターンが、１次式のパターンとほぼ同じになっています。
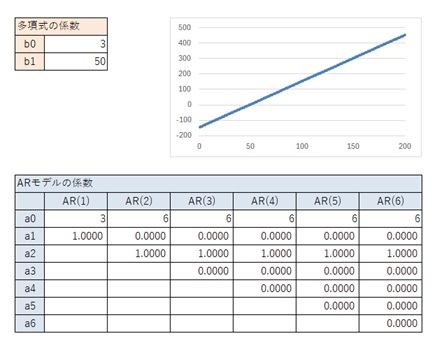
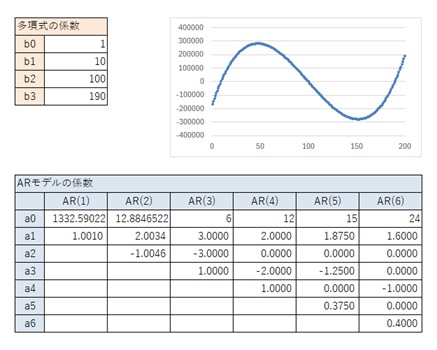
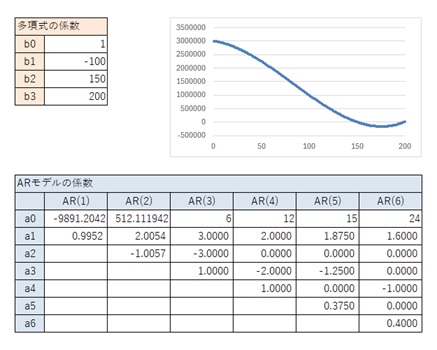
３次式の場合について、以下の結果をまとめると、AR(1)とAR(2)については、２次式の時とほぼ同じ値になっています。
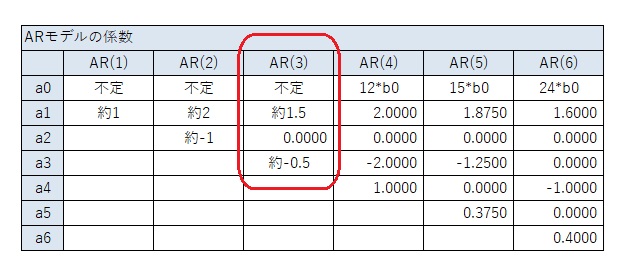
AR(3)については、３次式で典型的なパターン（3, -3 ,1）があります。 ただし、２次式の時のAR(3)のパターン（1.5, 0, -0.5)になることがあります。
AR(4)とAR(6)については、パターンが２種類見つかっています。 AR(5)については、パターンが１種類(1.875, 0, -1.25, 0, 0.375)見つかっています。
以下の結果から、一般的な３次曲線の場合は、上の表が結論です。
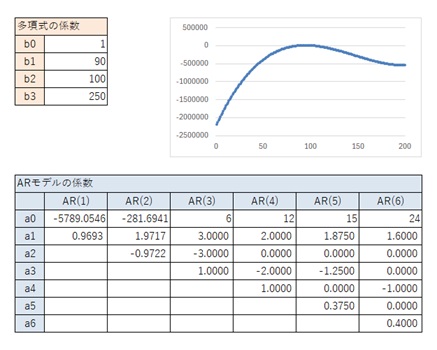
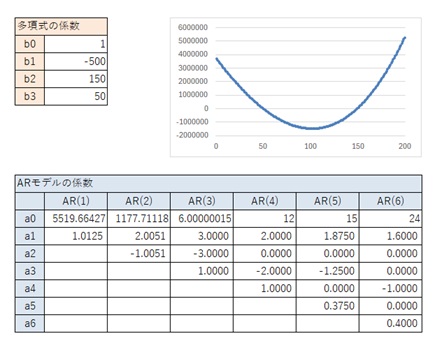
以下の結果から、AR(3)がAR(2)と似ているパターンがあることがわかります。
AR(4)以上では、一般的な３次曲線の場合と同じです。
見た目が２次曲線に近いと、このようになりやすいようです。
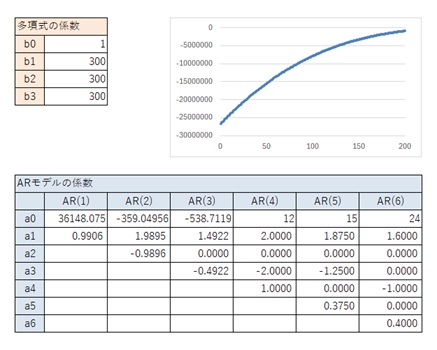
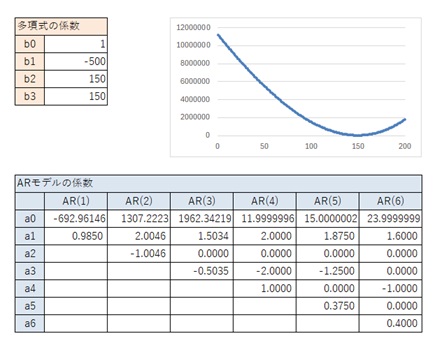
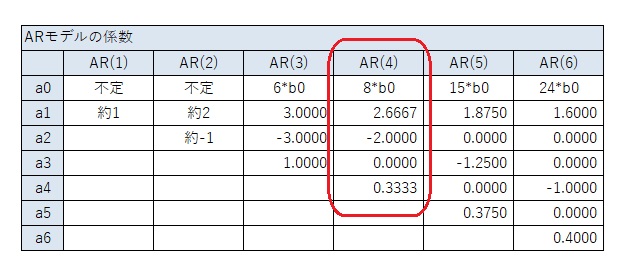
AR(4)の時だけが、一般的な３次曲線の場合と異なるパターンもあります。
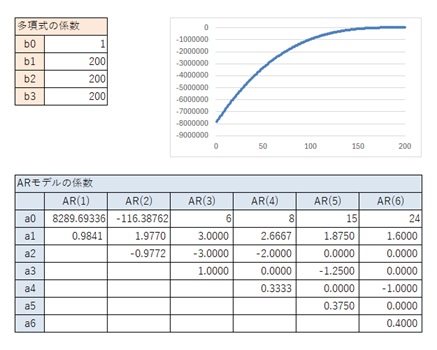
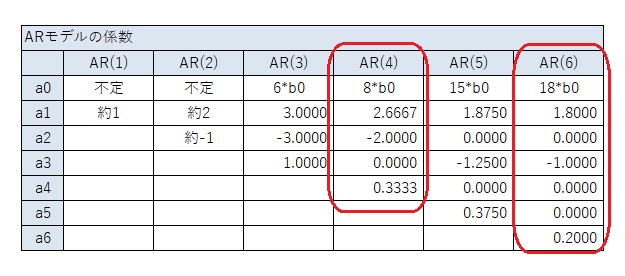
AR(4)とAR(6)の時に、一般的な３次曲線の場合と異なるパターンもあります。
この時の、AR(4)の値は、このひとつ前にある、AR(4)だけが異なる時と同じです。
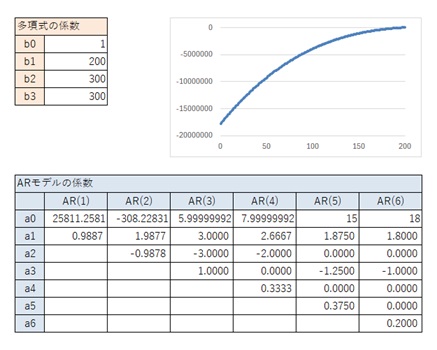
４次式の場合について、以下の結果をまとめると、AR(1)からAR(3)については、３次式の時とほぼ同じ値になっています。
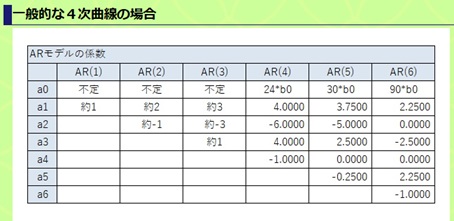
一般的な４次曲線の場合は、４次式ならではのパターンになっています。
それ以外については、３次式の時に見られたパターンに近いパターンが表れて来ています。
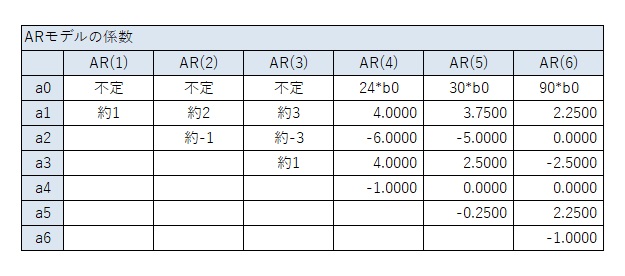
以下の結果から、一般的な４次曲線の場合は、上の表が結論です。
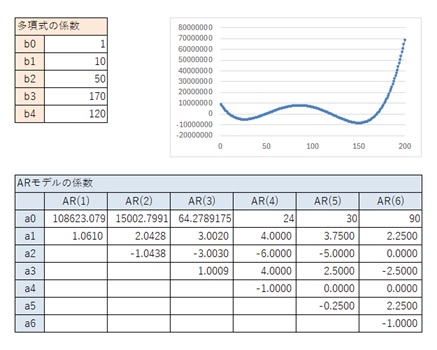
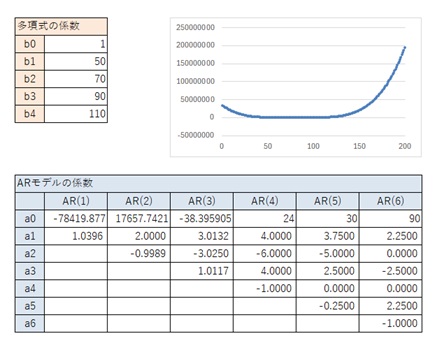
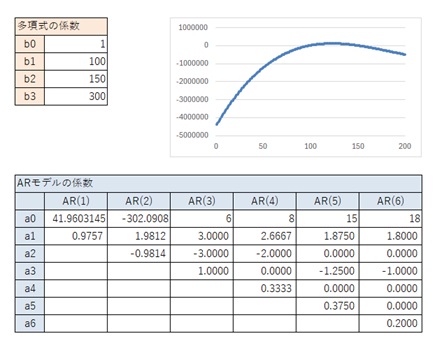
AR(6)が一般的な４次曲線と異なるパターンです。
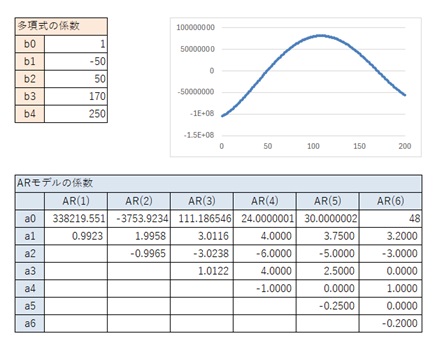
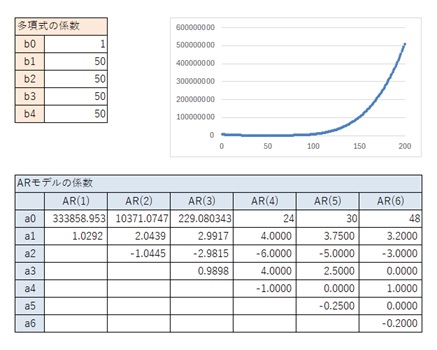
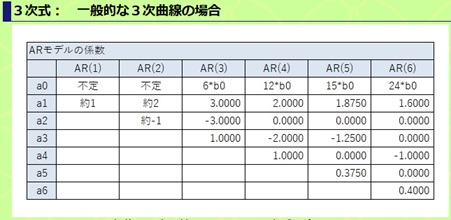
AR(1)からAR(5)までが、一般的な３次曲線と似ているパターンです。
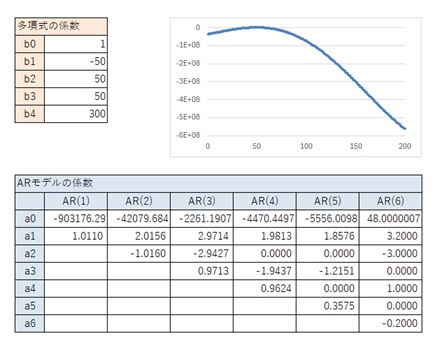
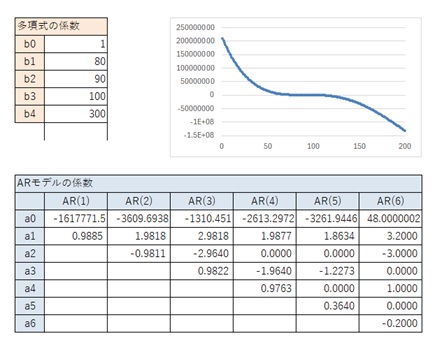
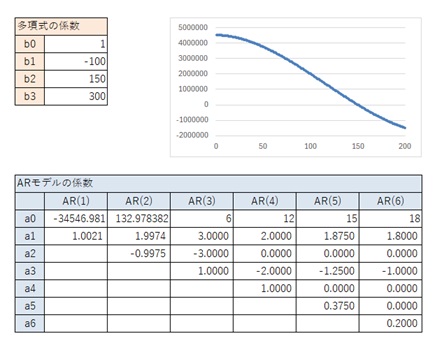
AR(1)からAR(6)までが、一般的な３次曲線と似ているパターンです。
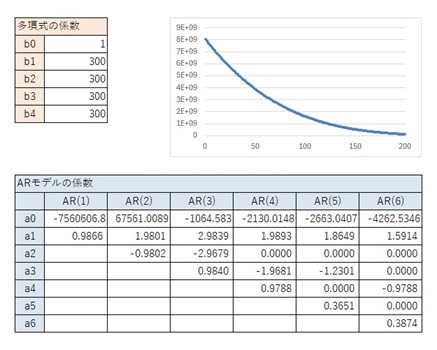
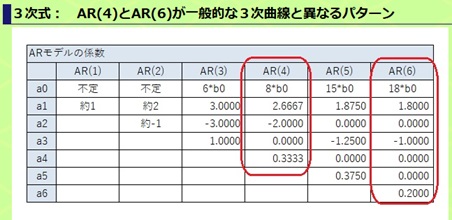
３次式で、似たパターンが出て来ています。
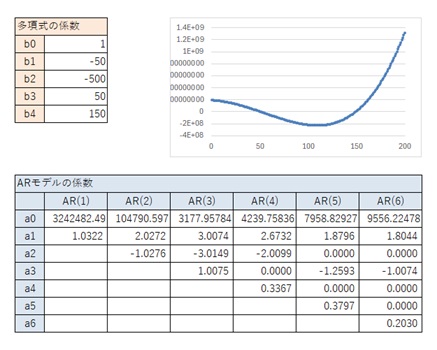
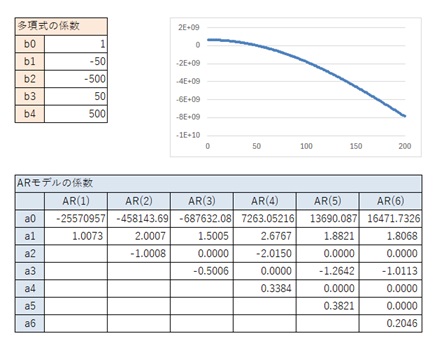
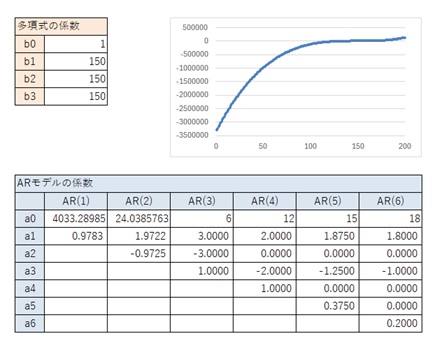
AR(4)とAR(5)のパターンは、３次式で似たパターンが出て来ています。
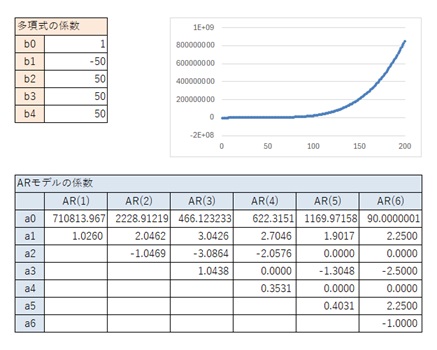
５次式の場合について、以下の結果をまとめると、AR(1)からAR(3)については、３次式の時とほぼ同じ値になっています。
一般的な５次曲線の場合は、５次式ならではのパターンになっています。
それ以外については、３次式の時に見られたパターンに近いパターンが表れて来ています。
以下の結果から、一般的な５次曲線の場合は、上の表が結論です。
４次式の時は、「典型的」といった感じのパターンがありましたが、５次式の時は、そういったパターンは、AR(5)までだけで、AR(6)については、不明確な感じです。
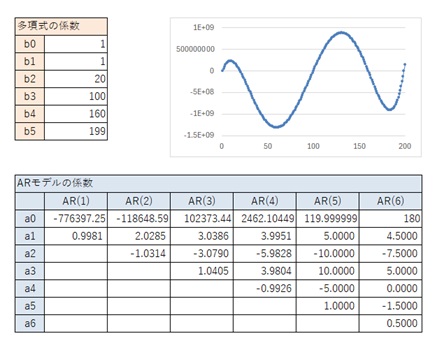
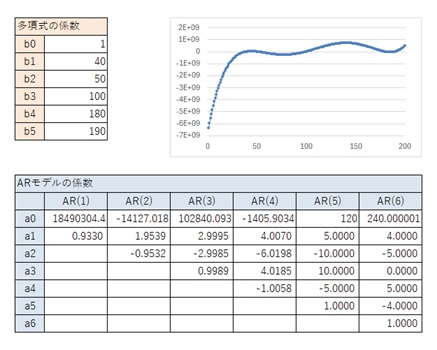
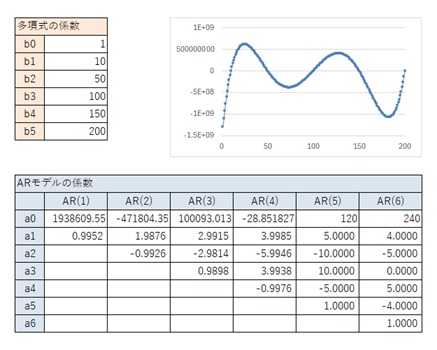
４次式の時までと同様に、一般的な５次曲線ではない場合は、異なるパターンになっています。
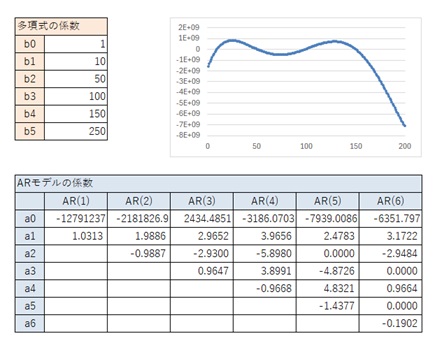
以下は、典型的な６次曲線のような場合の一例ですが、きれいな係数が求まらないです。 ５次式の時に、AR(6)が不明確になりましたが、６次式の場合は、AR(6)でも求まりませんでした。
この例の場合は、５次式の時に、似たパターンがあり、６次式ならではのパターンではないです。
