トップページ |
統計学の解釈学 |
このサイトについて
トップページ |
統計学の解釈学 |
このサイトについて
以下は、筆者の私見です。 誤解があれば、ご教示いただけると幸いです。
ARモデル は 時系列分析 の教科書で必ずと言って良いほど紹介されます。
このページでは、ARモデルについて、筆者が気が付いたことを説明します。 先行研究があるかもしれませんが、筆者は見かけたことがないです。
結論ですが、 ARモデルに合うデータの場合、AR(1)でも十分なこともあり、最大でもAR(3)までで見ておけば十分です。 逆に、AR(3)でも精度が低い場合は、ARモデルではそれくらいが限界なので、もっと大きくすることを考える必要がないです。
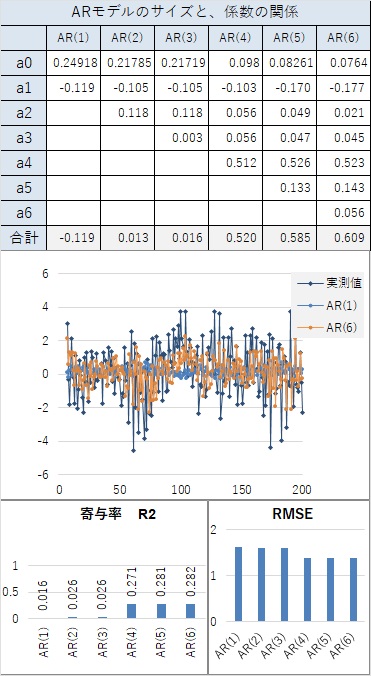
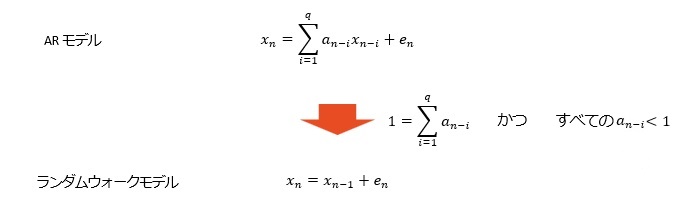
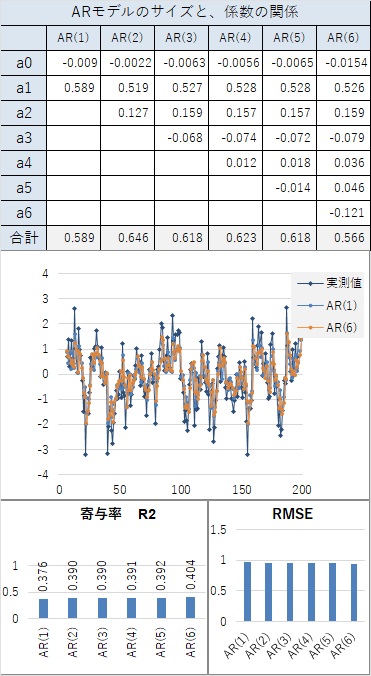
以下の場合は、AR(1)でも高い精度があります。
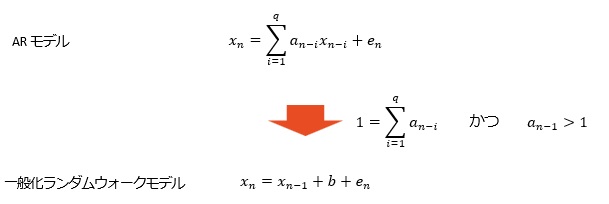
つまり、下記のようになっています。
AR(2)以上で、寄与率（相関係数の２乗）が1.000になります。 AR(1)でも、0.99以上あり、非常に高いです。
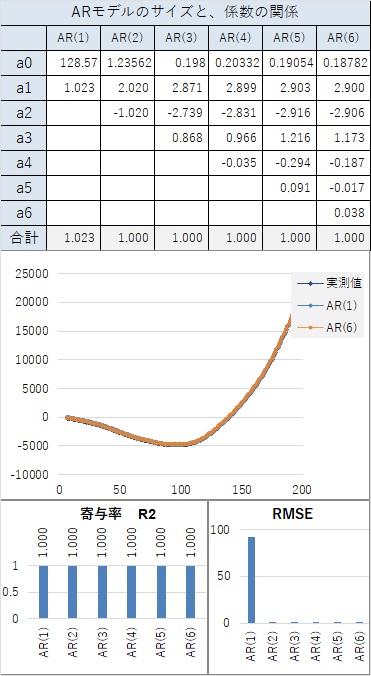
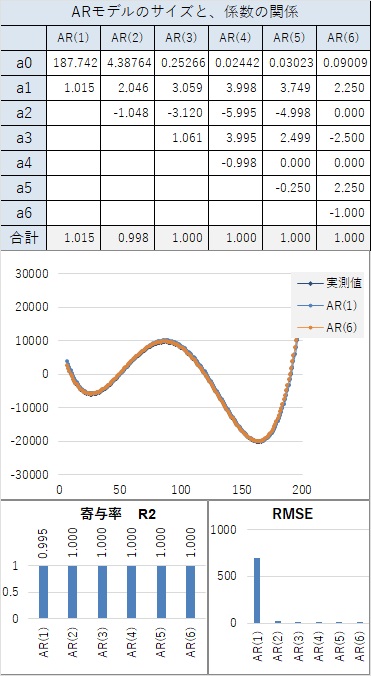
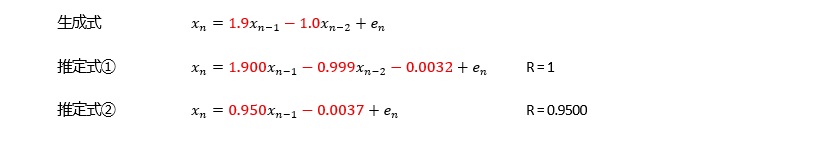
曲線と言えるほど、滑らかにつながっていなくても、隣接した値が近いと、AR(1)でも、寄与率が0.98以上になり、非常に高いです。
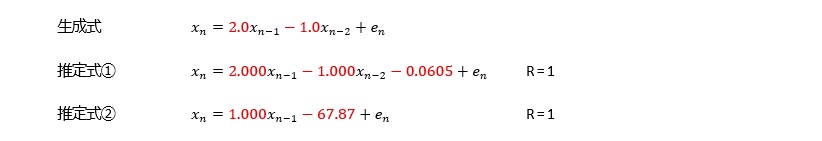
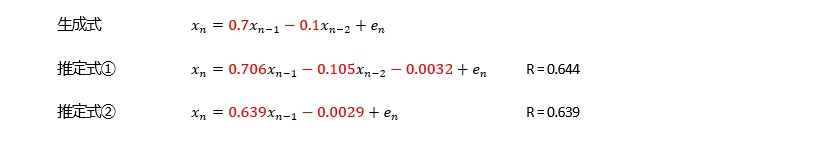
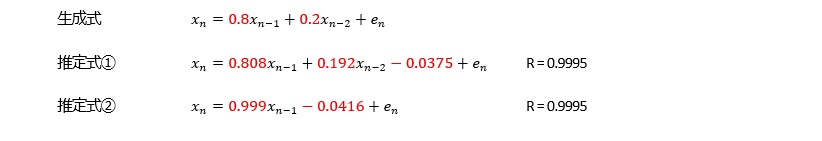
どうしてなのかは、筆者はわからないのですが、経験的に、ARモデルが合うデータの場合、AR(2)以上のa1の係数は、1以上になります。
ただし、直線上に上昇や下降する場合については、a1が1以下でも、精度が高いです。 直線上の場合は、a0が変化の大きさを直接的に表すことができるので、この現象が起きています。
変化が急な曲線の場合、AR(1)では十分ではないですが、AR(3)以上は大差ないので、AR(2)を考えておけば、良いです。
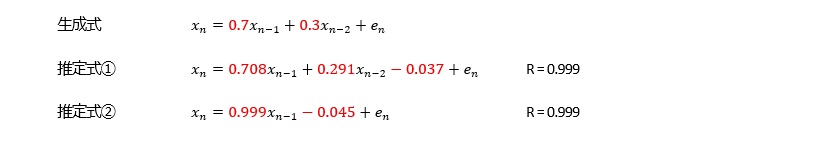
変化がさらに急な曲線の場合、AR(3)まで考えておくと、良いです。
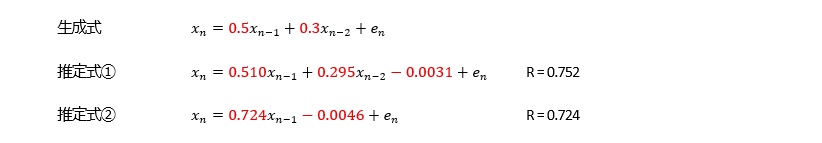
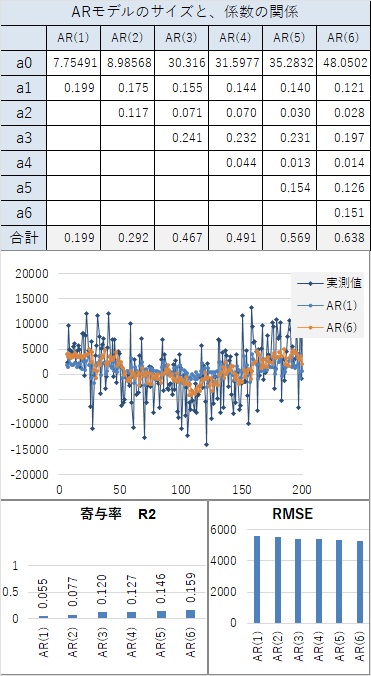
全体的にベースになるような変化が見えていても、そのベースからランダムにばらついているような場合は、精度が低くなりやすいです。
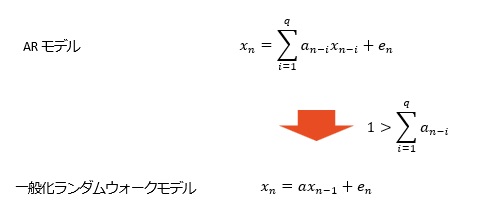
経験的に、この場合は、AR(2)以上のa1が1以上にならないです。
その場合、AR(1)と高次のARで精度が、あまり変わらない特徴があります。つまり、上記のケースとは別の意味で以下の式が成り立っています。
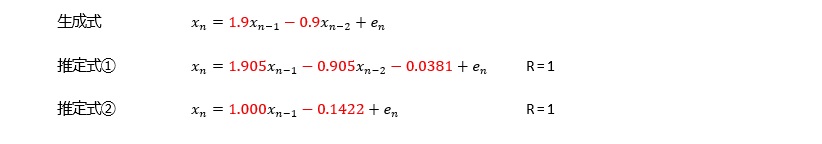
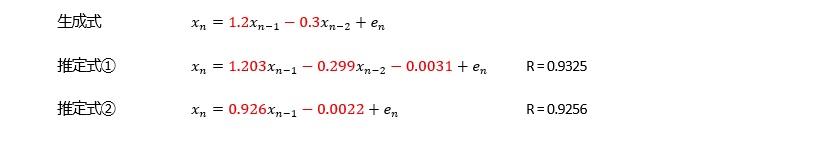
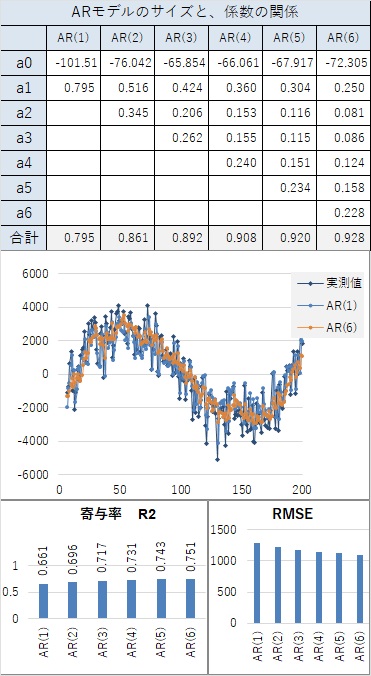
例えば、AR(6)というのは、６個前のサンプルまで遡ってモデルを作ります。 遡るそれぞれのサンプルに対して、係数をかけて足し合わせます。
例えば、周期が６の場合は、遡るそれぞれのサンプルではなく、６個前のサンプルだけを扱った方が良いです。 詳しくは 周期性とARモデルの関係 で説明しています。
以下の例は、周期が20になっています。
周期があったとしても、隣接した値が近いのなら、「隣接した値が近い場合」と同じことになるので、AR(1)でも、精度が高いです。
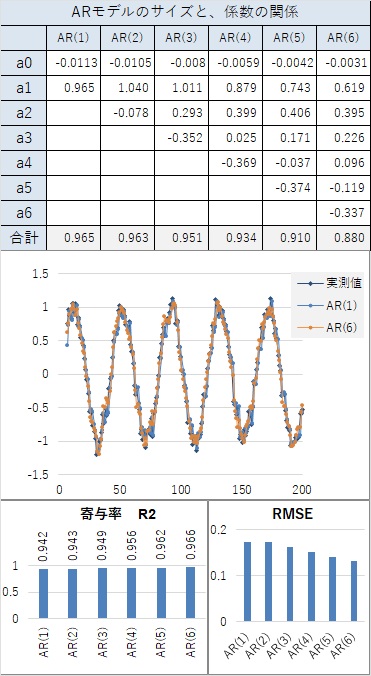
ところで、周期が20の場合は、以下の式で表現できます。
この式は、「20個前の値と近い」ということを表しています。
「隣接した値が近い」という情報はどこにも入っていません。
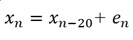
世の中に実際にある周期性では、周期性がある時は、隣接した値が近いことが普通ですが、 ここでは、周期性があっても、隣接した値が近くはない場合を考えます。
例えば、以下の例は、周期が６になる式で作られたデータです。
１周期前（６個前）のデータとは近いですが、隣接した値とは近くありません。
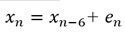
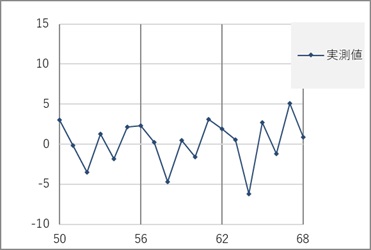
このデータの場合は、AR(6)以上で飛躍的に寄与率が上がりました。
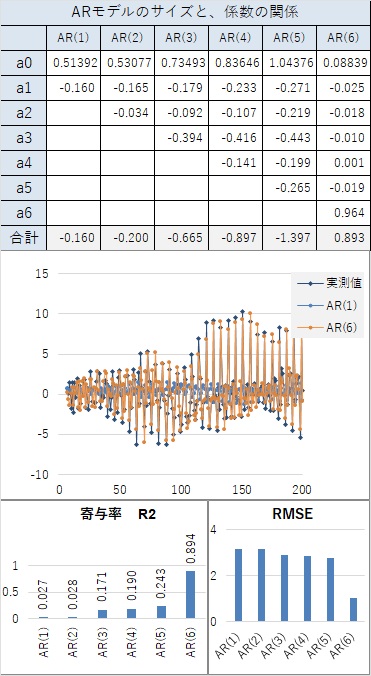
ふたつめのは、周期が４です。
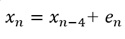
周期が４の場合は、AR(4)以上で、若干、寄与率が上がりました。
