以下は、筆者の私見です。 誤解があれば、ご教示いただけると幸いです。
このページのタイトルは、「帰無仮説は採択できる」です。 筆者は、「帰無仮説は採択できる」と考えています。
一方、世の中の多くの解説では、「帰無仮説は採択できない」です。
例えば、帰無仮説が「２つの平均値が等しい」、対立仮説が「２つの平均値は等しくない」だったとします。
この場合、有意水準を越えない時は、「『２つの平均値は、等しくないとは言えない』が正しい。 『２つの平均値は、等しい』は正しくない。」とする解説が、とても多いです。
「帰無仮説は採択できない」という考え方は、ひとつではないです。
以下では、諸説と、それらについての、筆者の見解を整理してみました。
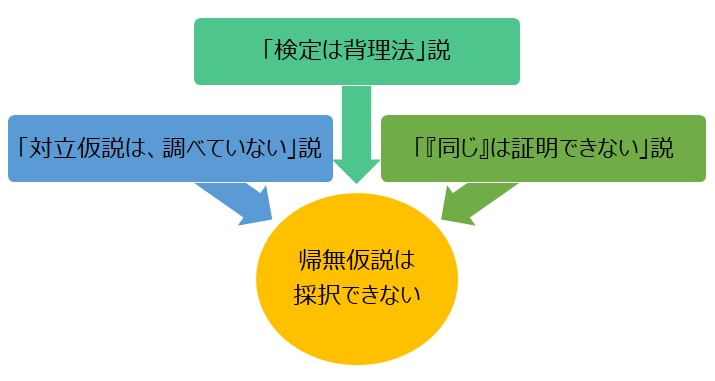
検定では、帰無仮説について、どのような位置関係なのかを調べるのが通例です。
「帰無仮説が棄却できない」という時に、「帰無仮説が採択できる」とした時に、実際は、対立仮説が真だった場合は、 第２種の誤り と呼ばれています。
これを知っていると、「帰無仮説が棄却できない」からと言って、「帰無仮説を採択」にはならないです。
２種類の対立仮説 について混同があり、「帰無仮説と対立仮説は、異なる分布に基づく」ということが念頭にあると起きる誤解のようです。
帰無仮説と論理的に逆（に近い）のものが対立仮説になっている場合、「対立仮説については、調べていない」ということは起きていないです。 つまり、第２種の誤りがないです。
そのため、「帰無仮説が棄却できない」なら、「帰無仮説を採択」になります。
帰無仮説と対立仮説の検定 のページがありますが、帰無仮説と対立仮説で、分布が異なる場合は、両方に対して、検証してしまうのが、一番直接的な方法です。
帰無仮説と対立仮説で分布が２つあるのに、帰無仮説側の作業だけで、分析を済ますことには無理があると思うのですが、 サンプル数を固定する統計学 と混同してしまって、対立仮説側は調べない場合が多いようです。
２つの分布に対して調べれば、「帰無仮説を採択」という結論もあり得ます。
検定では、対立仮説が成り立つことを説明するために、「得られたデータに対して、帰無仮説が成り立っていることは、とても考えにくい。 だから、帰無仮説以外のことが成り立っているのだ。だから、対立仮説が成り立っているのだ。」と考えます。
これを「背理法」と考えると、対立仮説が成り立つことは検証しているけれども、帰無仮説が成り立つかどうかは何も調べていないことになります。
背理法では、矛盾を示せれば証明になります。 矛盾を示せない場合、矛盾がないから示せないのか、矛盾を思い付けないからなのかがわかりません。 そのため、背理法なら、矛盾を示せないからと言って、逆が成り立つことの証明にはならないです。
検定は、背理法と似ていますが、背理法ではないです。
対立仮説が成り立つことの証明の方法は、背理法とほぼ同じです。 有意水準によって、白黒が決まるので、「ほぼ」としました。
検定では、データを元にして判断します。 成り立つかどうかは、データに依存します。 そのため、対立仮説が成り立たない時は、「矛盾を示せない」の一択です。 そのため、「帰無仮説を採択」という結論にできます。
「違う」かどうかは、違いを見せれば証明になります。
一方、「同じ」については、仮に何かが同じことを示したとしても、「それ以外の事も同じことの証明にはならない」と主張し始めると、証明する手段がないです。
例えば、猫と犬について、体重のデータを100匹ずつ用意して、平均値の差の検定をしたら、有意水準を越えなかったとします。
この結果の意味は、「（用意したデータでは）、体重に差はない」で良いと思います。
この結果に対して、「猫と犬は、動物学的に同じもの」と言ったら、それは行き過ぎです。 もしも、そのような結論を出している論文があれば、正しくないですが、「（用意したデータでは）、体重に差はない」は、真実です。
「統計学的に同じ」 という考え方がないです。
