主成分分析のルート や 多次元尺度構成法 に距離行列から内積を求めて、固有値分析をすると、主成分分析になる話がありますが、 それを実際にやってみた例です。
実務の場合は、このページの手順ではなく、 Rによる距離行列の位置分析 にあるように、距離行列を入力データとして、多次元尺度構成法などを進めた方が、簡単です。
このページは、Rのライブラリだと、cmdscaleと同じになります。
距離行列から内積を求める方法の検証です。
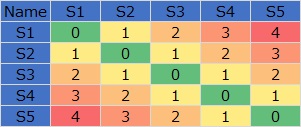
この例では、サンプルがS1からS5まであり、空間に１直線状に並んでいる場合の距離のデータです。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Distance <- as.matrix(read.csv("Data.csv", header=T,row.name=1) )
D2 <- Distance^2
A2 <- colMeans(D2)
A3 <- rowMeans(D2)
A4 <- mean(D2)
Inner_product <- (-1/2)*(t(t(D2)-A3)-A2+A4) # 距離行列からの内積の計算
eigen_value <- eigen(Inner_product)$value # 固有値
round(eigen_value / sum(eigen_value),4) # 寄与率
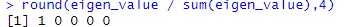
固有値は、サンプルの数と同じ数が作られるので、５つ出力されます。
寄与率は、最初の１個で1(100%)なことがわかります。
１直線状なので、これで合っています。
距離行列から内積を求める方法の検証です。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
n <- ncol(Data)
for (i in 1:n) {
Data[,i] <- Data[,i]-mean(Data[,i]) # 中心化の場合
#Data[,i] <- (Data[,i]-mean(Data[,i]))/(sd(Data[,i])) # 標準化の場合
}
Data <- as.matrix(Data)
Distance <- as.matrix(dist(Data))
D2 <- Distance^2
A2 <- colMeans(D2)
A3 <- rowMeans(D2)
A4 <- mean(D2)
Inner_product <- (-1/2)*(t(t(D2)-A3)-A2+A4) # 距離行列からの内積の計算
Inner_product
Data %*% t(Data) # 直接求めた内積
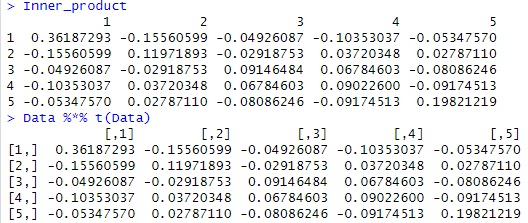
確かに、同じになりました。
