Rによるグラフィカルラッソ
変数の類似度の分析
です。
因果関係の分析をする時などは、総当たりの散布図は必要なく、１つの変数と他のすべての変数の組み合わせについて、散布図を見たいことがあります。
その時の作り方です。
グラフィカルラッソ＋ネットワークグラフ
グラフィカルラッソ
をしてから、ネットワークグラフにする方法です。
library(dummies) # ライブラリを読み込み
library(glasso) # ライブラリを読み込み
library(igraph) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- dummy.data.frame(Data)# 質的変数はダミー変換
DataM <- as.matrix(Data1) # テーブルデータを行列にする
COR <- cor(DataM) # 相関係数行列を計算
RHO <- 0.2 # スパース性を調整するパラメタ
GM1 <- glasso(COR,RHO)$wi # GMを実施（数値が大きいほどスパース。数値は結果を見ながら要調整）
# ここからは、グラフの描画用のデータの作成
diag(GM1) <- 0 # 対角成分は0にする
GM2 <- abs(GM1) # 絶対値にする
GM2max <- max(GM2) # 要素の最大値を求める
GM3 <- GM2/GM2max*10 # 一番大きな値が10になるように修正（パスの太さを指定するため）
GM3[GM3<5] <- 0 # 5未満の場合は0にする（非表示にするため）
rownames(GM3) <- rownames(COR) # 行の名前を追記
colnames(GM3) <- colnames(COR) # 列の名前を追記
GM4 <- graph.adjacency(GM3,weighted=T, mode = "undirected") # グラフ用のデータを作成
plot(GM4, edge.width=E(GM4)$weight) # グラフを作成
グラフィカルラッソのパラメタの決め方
グラフィカルラッソのプログラムでは、RHOの値の大きさで、
スパース性が変わります。
つまり、どのくらいのパスが0になるのかが決まります。
R-EDA1
では、自分で目盛りを調整して、分析できるようにしてあります。
RHOとパスの数を調べるためのプログラムを作ってみたのが、下記になります。
サンプルデータ
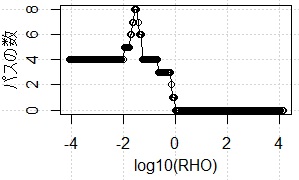
の場合は、下のようなグラフができます。
横軸は常用対数にしています。
log10(1)が0以上、つまり、RHOが1以上だと、パスが0になることがわかります。
library(glasso) #事前にパッケージ「glasso」をインストールしないと、エラーになる
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.table("Data.csv", header=T, sep=",") # データを読み込み
DataM <- as.matrix(Data) # テーブルデータを行列にする
COR <- cor(DataM) # 相関係数行列（標準化した共分散行列）を計算
x <- matrix(1:600, nrow=200, ncol=3) # 出力結果の入れ物を作る
for(i in 1:200){ # 200回繰り返す
RHO <- 1.1^(i-100) # iを使って段階的にRHOの値を作る
GM1 <- glasso(COR,RHO)$wi # GMを実施
diag(GM1) <- 0 # 対角成分は0にする
GM2 <- abs(GM1) # 絶対値にする
GM2max <- max(GM2) # 要素の最大値を求める
GM2max[GM2max==0] <- 1 # 最大値が0の場合、1にする（この値を分母に使うため）
GM3 <- log10(GM2/GM2max*1000)*3 # 一番大きな値が9になるように修正（パスの太さを指定するため）
GM3[GM3==-Inf] <- 0 # 0の要素は、-Inf に変換されているので0にする
GM3[GM3<0] <- 0 # 対数がマイナスになった値は0にする
GM3[GM3>0] <- 1 # 値が0よりも大きければ1にする（この後で数えるため）
x[i,1] <- RHO # RHO
x[i,2] <- log10(RHO) # RHOを常用対数にする（グラフのX軸に使う）
x[i,3] <- ceiling(sum(GM3)/2) # 値の入っている要素は1なので、この数の和がパスの数になる。2つの方向があるので2で割る
} # ここまでを繰り返す
write.csv(x, file = "RHO.csv") # 結果をファイルに出力
plot(x[,2],x[,3],xlab="log10(RHO)",ylab="パスの数",type="o",panel.first=grid()) # グラフを作成
