warpbreaksは、実験のデータです。 羊毛（wool）が２種類（２水準）、張力（Tension）が３種類（３水準）あった時の、全部の組合せについて、切れた数がデータになっています。
このページは、 R-EDA1 で分析をした事例になります。
筆者は、下記のコードでデータを入手して、csvファイルにしています。
Cドライブ直下のRtestというフォルダに保存します。
write.csv(warpbreaks, row.names = FALSE, "C:/Rtest/warpbreaks.csv")
warpbreaks.csv のリンク先で、このサイト内に保存したcsvファイルをダウンロードできます。 なお、保存されているファイルは、「warpbreaks.csv」なのですが、「warpbreaks.xls」というファイルとしてダウンロードされ、 「拡張子がおかしい」という意味のエラーメッセージが出る現象があります。 ダウンロードされたファイルの拡張子を「xls」から「csv」に変更すれば、問題なく使えるようになります。
ここからは、任意の場所にある「warpbreaks.csv」というファイルを使っています。
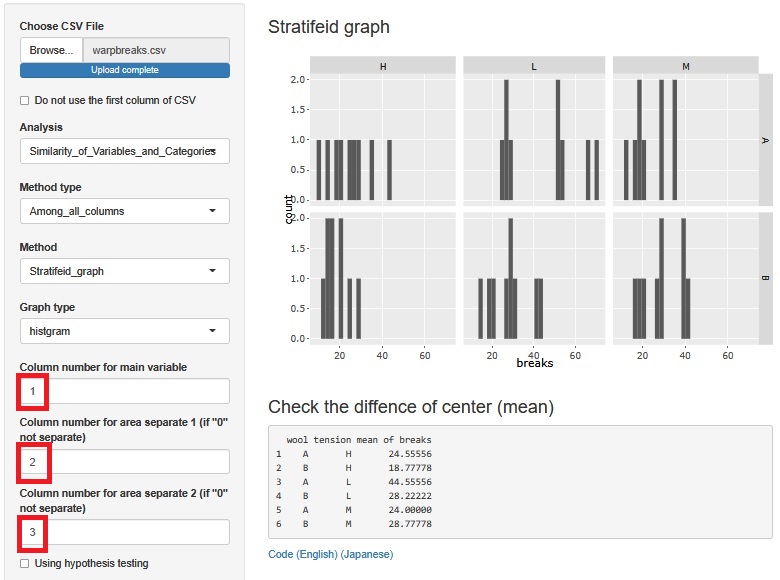
２つの因子を使って、層別のヒストグラムを作成します。
条件によって、平均値が異なる感じです。
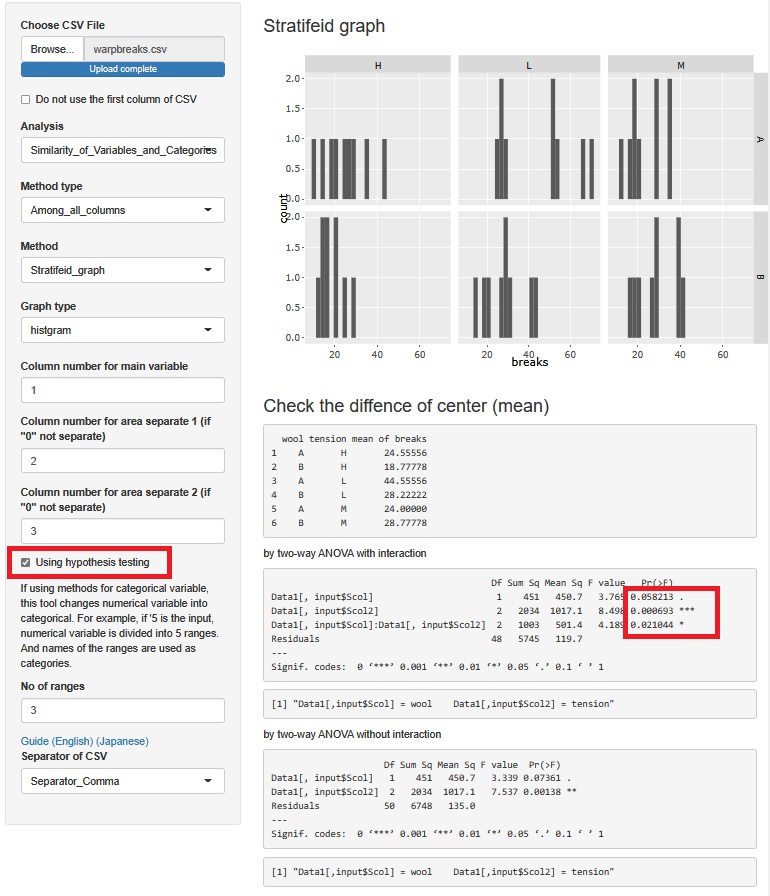
「Using hypothesis testing」にチェックを入れると、 分散分析 の結果がグラフの下に出て来ます。
p値のPr(>F)のところを見ると、*が付いています。 付いていないものについても、0.1よりは小さいです。 そのため、２つの因子はどちらもbreaksに影響していると考えられます。 「Data1[, input$Scol]:Data1[, input$Scol2]」も*がひとつなので、交互作用もあると言えます。
なお、 ビッグデータの統計学 にあるように、昨今の統計学の考え方では、p値で結果を判断することはしなくなって来ていますが、 筆者としては、このくらいのサンプル数のデータなら、p値が0.05くらいを目安にして、効果の有無を議論するのは良い進め方と思います。
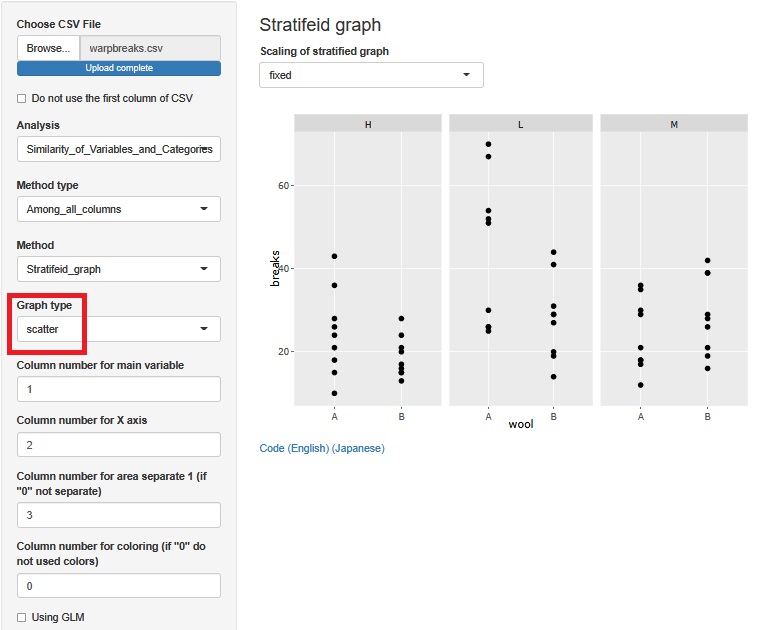
今度は散布図にします。
わかることはヒストグラムと同じですが、 HとLの時は、Aの方がBよりも平均値が高めなのに、Mの時は、Bの方が高めなのが、こちらの方がわかりやすいです。 また、HとLの時は、AよりもBの方がばらつきが小さいことも、こちらの方がわかりやすいです。
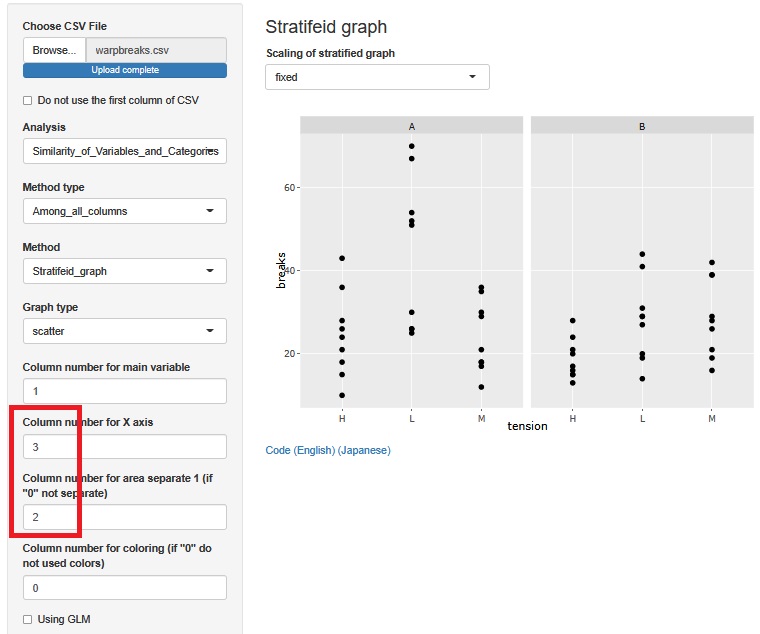
層別の変数を変えます。 すると、「Hの時に、AもBもbreaksが低いことは共通」、「Aでは、HとMに差がなさそうで、Lだけ高め」、「BではLとMに差がなさそうだが、Hだけ低め」となっていることがわかります。
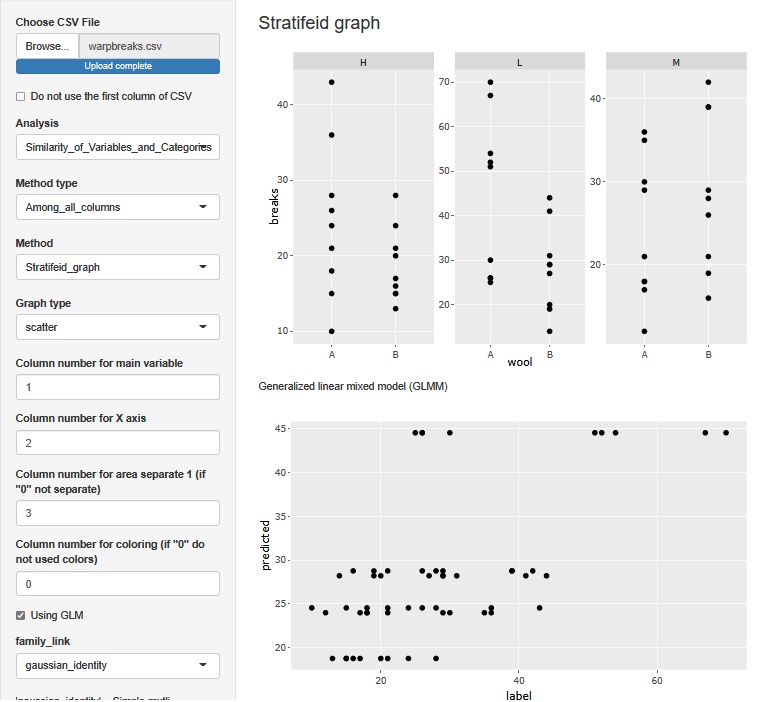
「Using GLM」にチェックを入れて、 重回帰分析 をします。 この場合は、説明変数が質的変数なので、 数量化I類 と同じです。
層別の１次元散布図の下に、２次元散布図ができます。 この散布図は、横軸がlabel（この場合は、breaks）の元のデータの値です。 縦軸が、labelの予測値になります。 predictedの値が大きいほど、labelのばらつきが大きくなっています。
重回帰分析でわかることは、分散分析と同じです。
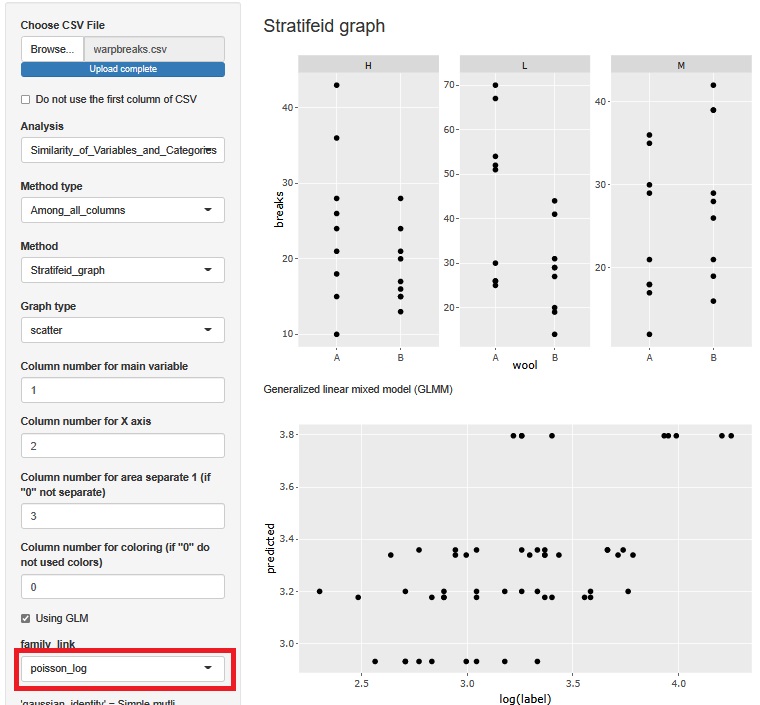
「Using GLM」の機能は、 一般化線形混合モデル なので、 ポアソン回帰分析もできます。 この場合は、「family_link」を「poisson_log」にします。
重回帰分析の時は、predictedの値が大きいほど、labelのばらつきが大きくなっていましたが、 そういうことはなくなったので、こちらの方が良いようです。 ポアソン回帰分析の方が、重回帰分析よりも良い理由は、 breaksは計数値であり、また、平均値が大きい時はばらつきが大きい性質があるからと考えられます。
上記の機能は、層別の散布図に選んだ変数だけで、一般化線形混合モデルを作るようになっているので、 もっと変数が多くなるとモデルが作れないです。 R-EDA1では、一般化線形混合モデルは、別の機能でもできます。 この機能の場合は、層別の散布図は作れないのですが、変数が多くても全変数を使ったモデルを検討できます。
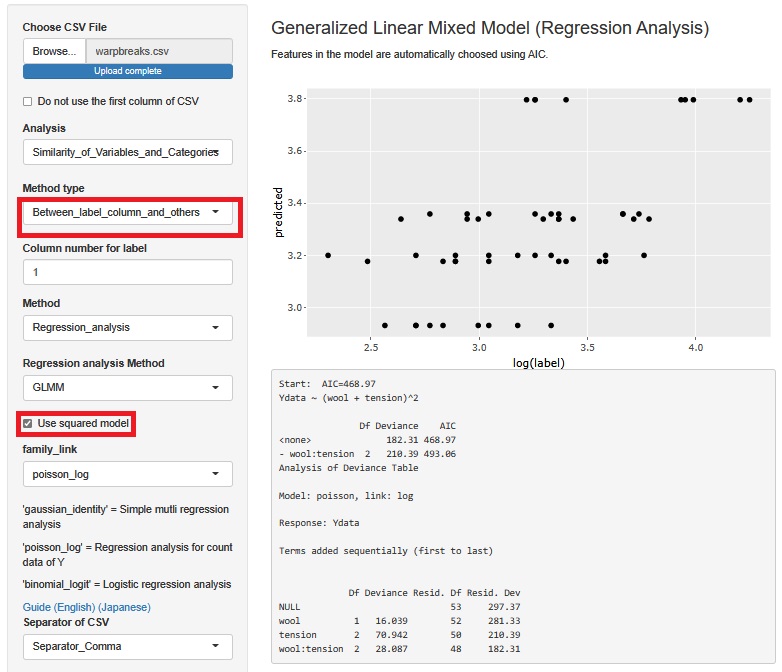
この例は、ポアソン回帰分析の場合です。
層別の散布図の機能では、交互作用項をモデルに必ず入れるのですが、この機能の場合は、 「use squared model」にチェックを入れると、交互作用項が入ります。
分析によって、warpbreaksの実験の２つの因子はいずれも重要で、交互作用の効果もあることがわかりました。
つまり、羊毛の２種類は、単純にどちらかの方が、張力に強いわけではなく、張力の範囲によって、優劣が変わることがわかりました。
この結果は、１次元の散布図で視覚的に確認できるものですが、分散分析や、一般化線形混合モデルを使った確認もできました。
Rのデータセット
warpbreaks以外についても、網羅的に紹介しています。
https://www.math.chuo-u.ac.jp/~sakaori/Rdata.html
Tweet
