区間推定

平均値や標準偏差のような統計量がありますが、これらの計算は、統計学的には「点推定」と呼ばれています。

点推定よりも考え方が難しいのですが、「区間推定」というものもあります。

信頼区間と確信区間

信頼区間と確信区間は、ある確率での統計量の範囲を推定する方法です。

予測区間は、個々のデータの推定です。

予測区間は、外れ値の判定や異常値の判定に使えます。

学問としては、予測区間よりも信頼区間の方が注目されやすいようです。そのためか、信頼区間は計算する機能はあるのに、予測区間は計算してくれないソフトはあっても、逆はありません。

サンプルが５個あった時に、信頼区間と予測区間をそれぞれ95%で計算すると、下のグラフのようになります。

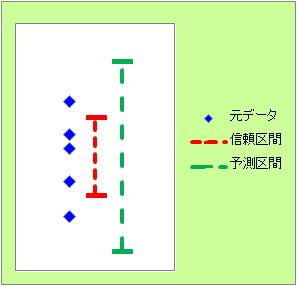
信頼区間は、平均値の位置を示しています。予測区間は、データの範囲を示しています。