トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
予測の基本は、「次のデータは、いくつか？」という予測です。
その次のレベルとして、大きく分けて2つの方向性があります。
「次の次のデータは、いくつになるか？」という予測と、
「次のデータのばらつきは、いくつか？」という予測です。
異常検知 として、異常を予測する方法は、予測の種類によって、違っています。
まず、「次のデータは、いくつか？」という予測による異常検知です。
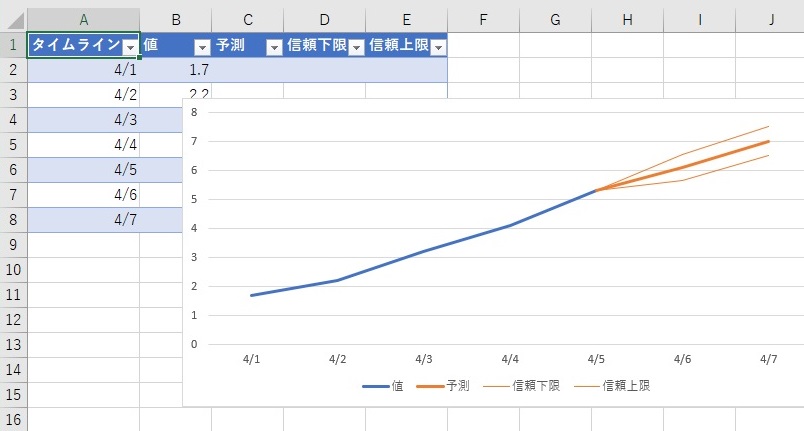
例えば、2025年1月まで予測して、下のグラフだったとします。
危険ラインが65の場合、「正常の範囲内」という判断ができます。
次に、「次のデータの、ばらつきは、いくつか？」という予測による異常検知です。
まず、上のグラフで求めた予測値について、二乗平均平方根誤差（RMSE）の3倍を加えたデータと、引いたデータを作ります。
「二乗平均平方根誤差の3倍」とは、製造業の品質管理で「3シグマ」と呼ばれて使われている管理値の目安です。「3シグマ」は、「3σ」と書くこともあります。英語の読み方では、「スリー シグマ」ですが、筆者の周りでは、「さん シグマ」と読む人の方が多いです。
データが正規分布の場合、中心のプラス側とマイナス側のそれぞれに対して、3シグマで作った範囲には、データの99.7%が入ります。
作ったデータをグラフに加えると、下のグラフになります。
約99.7%の範囲の内側に危険ラインがあるため、「2025年1月は、危険ラインを超えるかもしれない。」という予測ができます。
この例のようなデータの場合、次のデータの中心値を予測しても、その通りにならないことが普通です。 危険ラインよりも内側に外れてくれるのなら問題が起きませんが、外側に外れるのは困ります。
ばらつきも考慮して、範囲で予測すると、その範囲よりも外れることは、非常に起きにくいです。 そのため、範囲の予測は、とても頼りになる予測になります。
最後に、「次の次のデータは、いくつか？」という予測による異常検知です。予測値をさらに延長すると、下のグラフになります。
2025年1月は、予測値の中心は危険ラインを超えず、予測値の上側は危険ラインを超えていましたが、2月以降は、予測値の中心も危険ラインを超えることがわかります。
「次の次」というように、時間的な観点がある場合は、 時系列分析 の出番です。
なお、時系列分析の本でよく紹介されている ARMAモデル や ARIMAモデル などの ARモデル の系統は、基本的に「次の次」という予測ができません。 例外として、完全に多項式や三角関数に一致する曲線の場合は、ARモデルでも「次の次」の予測ができます。 また、周期性がある場合は、１周期先までの範囲なら、 SARIMAモデル は「次の次」の予測ができます。 （詳しくは、多項式とARモデルの関係、三角関数とARモデルの関係を参照してください。）
「次の次」の予測をするには、トレンドを捉えられるモデルを使います。 例えば、 時系列回帰分析 や 三重指数平滑法 があります。
Excelで三重指数平滑法
のページで詳しく説明していますが、
Excelでは、次の次以降のデータの予測を、ばらつきの範囲付きで簡単にできるようになっています。
順路
次は
測定
