平均値（Average ：アベレージ）は、 統計量 の一種です。
平均値は、全部のデータを足し合わせて、データの数で割った値です。 計算が単純ですし、集団を表す値として便利です。
しかし、現実のデータ解析では、平均値の扱い方が原因で、解析を失敗する場合があります。 代表的な理由は、２つあります。
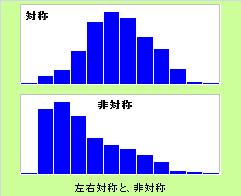
1・2の問題を簡単に解決する方法として、 中央値（メディアン・メジアン・Median）を平均値の代わりに使う方法があります。 中央値は、 箱ひげ図 でも使われています。
データが奇数個の場合、データを大きな順に並べた時の、真ん中の値が中央値です。 データが偶数個の場合、真ん中付近の２つの値の平均値が、中央値です。
中央値は、真ん中付近の値だけを使って求めるので、異常値が混ざっていても、 その値は中央値の算出に含まれません。 そのため、異常値の影響を受けません。 また、真ん中付近の値なので、分布が対称的ならば、中央値と平均値は、ほぼ同じになります。
奇数個と偶数個の使い分けですが、順番が真ん中になるデータを知りたい場合は、奇数個にする必要があります。 平均値の代わりに使いたい場合は、偶数個の方が、精度が良くなりやすいです。
中央値を知ってしまうと、どんな時でも平均値の代わりに使った方が良いような気もして来ますが、
データが非対称でも、平均値が必要な場合もあります。
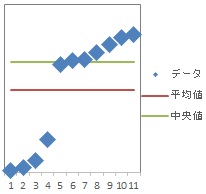
また、下図のようなデータの場合は、平均値の方が良いこともあります。
中央値を使うか、平均値を使うかは目的次第です。
1 のみの解決策としては、 データの最大値や最小値付近の値を平均値の計算から除外してしまう「トリム平均値」 という値もあります。 「トリム（trim）」とは、「切り取る」という意味です。
トリム平均値を実際に計算する時には、 「分布の裾の値なのか？異常値なのか？」という判断で困ってしまい、 平均値の計算から除外する値の選別が難しい場合があります。
２つ以上の集団の比較として、平均値の大小関係を議論するのは、いろいろな所で見かけます。 しかし、単純に平均値だけを比較するのは、失敗しやすいです。
失敗する原因のひとつが、上記のように異常値が混ざっていて、不適切な計算をしている場合です。
もうひとつの失敗する原因は、ばらつきの影響です。 ばらつきが大きいデータの平均値は、そのばらつきの仕方が、ちょっと変わっただけで大きく変動します。 そんな平均値の比較は、当てにならないです。
平均値の比較をする時は、 「ばらつきを踏まえて考えても、その平均値の差は、差があると言えるか？」 、というチェックが必要です。 このチェックは、ヒストグラムで視覚的にできます。
上記では、異常値が不要な時に、異常値の影響を取り除く方法を紹介しています。 しかし、 異常状態の工程解析 の時は、異常値が「なぜ異常になったのか？」を調べたりしますので、 いつでも異常値を無視して良いわけではないです。
異常値を無視しないケースでは、例えば、異常値と、異常値以外の値の、大きさの違いから、 異常原因を推測します。 また、異常値と異常値以外の値の、Xの違いから、異常原因を推測することもあります。
時系列解析 で便利な平均値の使い方に 移動平均 があります。
移動平均は、例えば、１時間毎に測定したデータがある場合、現在までの10時間分の平均値を１時間毎に計算したりします。
ノイズが多いデータを、滑らかにする方法として使われることもあります。
移動平均の考え方の応用をこのサイトでは、 移動分析 と呼んでいますが、複雑な関係性をシンプルに分析する方法や、 異常検知の方法として注目されています。
移動平均の計算でも、中央値やトリム平均値を代わりに使うこともできます。
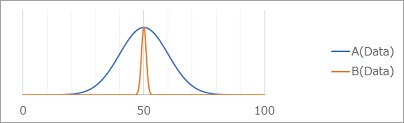
例えば、下のグラフのA、Bはどちらも平均値が50ですが、ばらつき方が違います。
「平均値が50点だから、レベルアップのために対策をしよう」となった場合、Bの場合は、皆同じくらいの点数なので、全員に対して同じ対策をする動きになります。
Aの場合は、30点、40点の人にだけ重点的に対策をする方法が良さそうです。全員に何かをするとしても、30点くらいの人と、70点くらいの人ではやることが変わります。
平均値は便利ですが、平均値だけを見て何かを始めると、うまく行かない事があります。
「平均値が上がったから、この対策は効果があった」と言うような話は、よくあります。 学問の世界や、会社では、それがその人の業績に影響することもあります。 その時に、Bのような分布の話をしているのなら、あまり問題がないのですが、Aのような分布の時は、その対策だけでは何も解決していないこともあります。
データや理論を使って、結果を説明すると、もっともらしく聞こえます。 しかし、そのデータはどのようなものか、その理論はどのようなものか、という事を抜きにして、一部だけが切り取られて 「成果があった」、「成果にならない」という議論になっているのは、よくあります。
なお、 平均値の差の検定 や 平均値の検定 を使うと、「平均値が50と言えるのか？」という評価はできますが、「Aではなく、Bなのだ」という評価はできないです。 現時点では、「Aではなく、Bなのだ」という評価は、グラフを使うのが無難です。
順路
次は
平均値の意味の使い分け
