比率の差の検定

比率の差は、とてもシンプルな指標です。百分率にして（100倍して）、「今回の選挙では、投票率が5ポイント上がりました」、といった感じで、ニュースなどでも使われる指標です。

ところで、 100／1000　と　400／2000の差と、1/10 と4 /20の差は、どちらも0.1です。

しかし、同じ0.1でも、0.1の信頼性や正確さは違います。比率の差の検定では、データの数も考慮して、「0.1」という数字に差があるといえるのかどうかを判定することに使います。

平均値の差の検定では、データのばらつきや数を考慮して、平均値に差があるのかを判定することと似ています。

このようなデータでは、薬の効果が評価したいです。比率の差の検定は、このような目的に使います。

なお、このようなデータの分析方法のひとつに独立性の検定がありますが、独立性の検定はデータの相関性を見るものなので、薬の効果の分析には使えません。

母不良率の差の検定

品質学の分野では、比率の差の検定は、「母不良率の差の検定」と呼ばれています。こちらの名前の方が、参考文献は多いようです。

ちなみに、有効数字を知っていると、
100／1000　＝　0.100
400／2000　＝　0.200
なので、差は0.100になります。また、
1／10　＝　0.1
4／20　＝　0.2
なので、差は0.1になります。

このように考えて、「同じ0.1でも、0.1の信頼性や正確さは違います。」とも言えます。

この考え方だと、
「8／80　と　8／40の差と、1/10 と 4/20の差」
については、「同じです」となります。

比率の差の検定をすると、p値（p-value）は、0.2171となります。結論は、有効数字の考え方と変わらないです。

有効数字で考える場合は、桁の数を使って比べるので、桁の数が変わるほど違わないと、違いがわからないのですが、比率の差の検定を使う場合は、p値を使えるので、データ数の細かな違いがわかります。

Rの実施例は、 Rによる違いの有無の分析のページにあります。

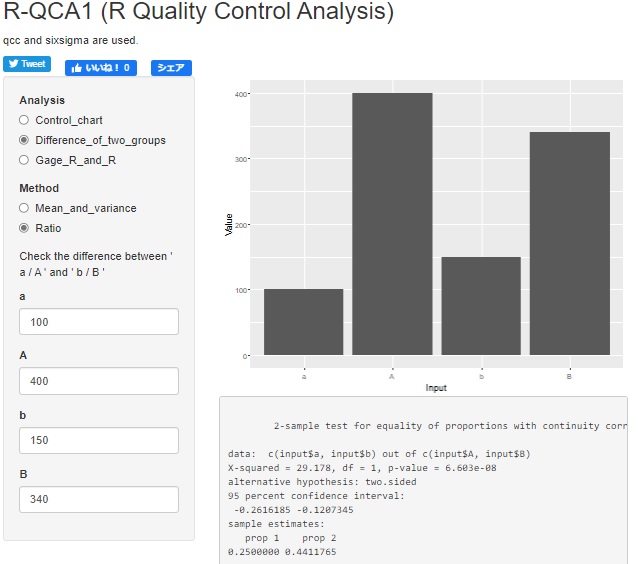
Rがインストールされていないパソコンやタブレットなど、手軽にやるには、 R-QCA1 が良いかと思います。必要な４つの数値を入力すると、グラフとセットで結果が出ます。
ウェブアプリ　R-QCA1

「SPSSによるリスク解析のための統計処理」　石村貞夫・石村園子　著　東京図書　2004
オッズ比の計算や、比率の差の検定など。