
A typical Regression Analysis assumes a simple formula and tries to find the parameters (coefficients) of the formula so that it fits best.
Splines seek complex formulas, rather prioritizing good data fits.
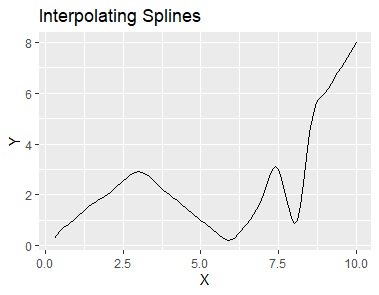
Spline interpolation is a method of drawing a curve that smoothly connects all the samples. The figure below is made with Excel.

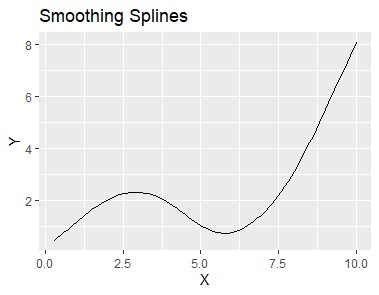
Smoothing splines are a method between spline interpolation and regression analysis. Depending on how you set the parameters, you can achieve the same result as either one.
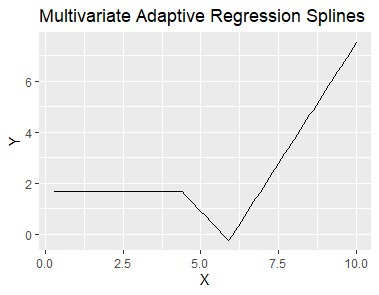
Multivariate Adaptive Regression Splines (MARS) is a companion to "splines", but unlike the above two types, it outputs mathematical formulas.
If you have a simple rule for arranging the data, it's a simple formula. It's a method that is somewhere between the general regression analysis and the above two types.
Multivariate adaptive regression splines try to fit the sum of the hinge functions. Since the hinge function contains elements that perform regression analysis
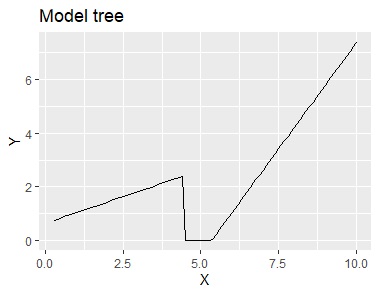
The Model tree divides the data into intervals and can produce the results of general regression analysis for each interval.
Multivariate adaptive regression splines are the same in that they contain elements for regression analysis in intervals.
The difference between the two is that in the model tree, the formula is calculated only for the data in that interval, whereas in the multivariate adaptive regression spline, the formula is applied to all the data. increase.
In Deep Learning , the ReLU function (ramp function) may be used as the activation function.
The hinge function used in multivariate adaptive regression splines and the ReLU function are very similar. The ReLU function is the hinge function when the origin is limited to the bending point.
With that in mind, it seems good to think that "multivariate adaptive regression splines have one layer in the middle layer in deep learning and the activation function is ReLU".
From left to right are data, spline interpolation, smoothing splines, multivariate adaptive regression splines, and model trees.

An example of R can be found in Spline by R .
NEXT 

 Label Classification
Label Classification
