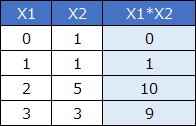
The interaction term is a method for dealing with interactions in multiple regression analysis, etc.
An interaction term is a new variable created by multiplying two variables. It is a type of feature engineering.
"Why make a product?" and "What is the meaning of the product?" If you start thinking only about this, you will not understand well, but if you use this as a variable, It has an interesting nature.

Multiple regression analysis is an introduction to using
equations such as: If this equation is accurate, you don't need to think about interaction terms for your data.
Analyzing the importance of a variable is an introductory step in investigating whether X1 or X2 has a stronger influence on Y. If you can add up one variable, or even multiple effects, you don't have to think about interaction terms.
Interaction terms are useful when both X1 and X2 are important, and there are features that are not just the sum of X1 and X2.
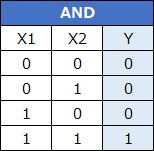
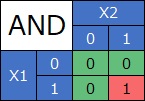
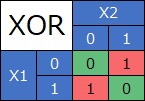
For the AND condition, the product (multiplication) of X1 and X2 and the value of Y are the same. In the case of OR and XOR, the sum or product of X1 and X2 does not give Y.
A new variable that is made by the product of two or more variables is called an interaction term. The product of variables is the same, but the properties of interaction terms are quite different from AND.
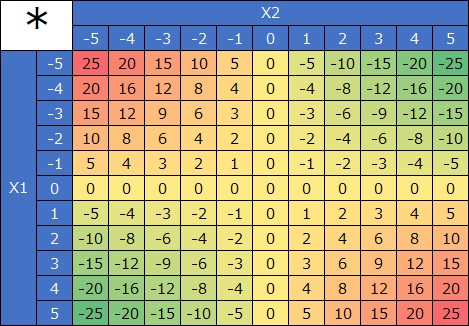
The heatmap on the left is the product of the variables X1 and X2. The 3D graph on the right shows the same data as a surface plot. As both numbers increase, the numbers become so large that they cannot be thought of by mere addition. The phenomenon of "synergy" applies.
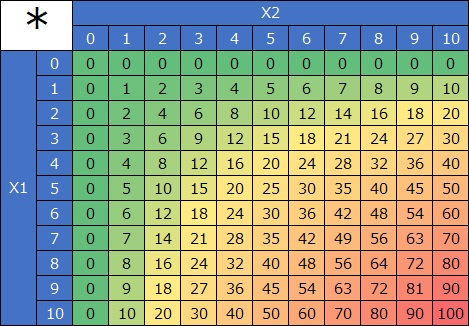
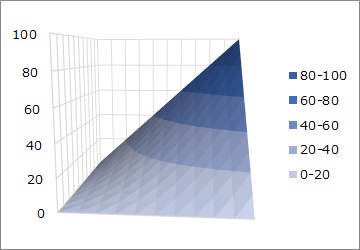
If one is 0, Y is 0 no matter how large the other is the same as the AND condition. Also, if you cut off only the upper left part of this table, you will get the AND condition itself. In this sense, only positive numbers can be considered an extension of the AND condition.
If it is only the property that "the larger the number of X, the greater the increase of X", it can be expressed by one X squared. Interaction terms can express properties similar to AND conditions.
Depending on how the X range is taken, the characteristics will change. In the lower case, when X1 is negative, the larger X2 is, the smaller the Y, but when X2 is positive, the larger X2 is, the larger the Y.

Since the characteristics of this graph are similar to the XOR condition, the interaction term can handle phenomena similar to the XOR condition.
If only the property is that "the larger the number of X, the more X increases in the positive direction or the negative direction", it can be expressed by one X squared. An interaction term allows us to express that the value of another variable changes direction.
Incorporating the properties of interaction terms described above into multiple regression analysis to model complex data is the first step in using interaction terms. Simple regression analysis with one variable allows you to handle things that could not be expressed no matter how complex you do.
Multiple regression analysis that includes X1 and X2 squared and interaction terms X1*X2 when there are variables X1 and X2 is called a "quadratic model".
The Response Surface Method used in the analysis of experimental data is this model.
The properties of interaction terms can be further applied if you use them creatively.
If Y can be represented by 1 and 0, you can use Logistic Regression. Interaction terms can help you handle distinctive data.
This is the case for distributions such as the AND condition. The left is the original data, the middle is the predicted value created by the model with no interaction term, and the right is the predicted value with interaction term. At first glance, it seems that the one with the interaction term is better, but this is not necessarily the case because the predicted value of the lower left area is not 0.

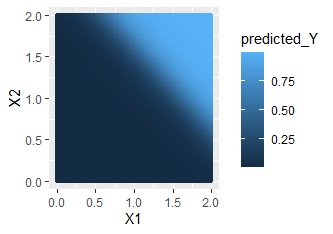
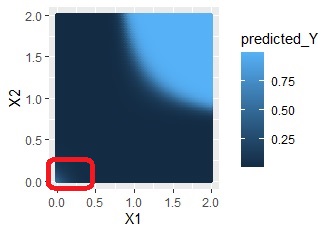
This is the case with distributions like OR conditions. At first glance, it seems that the one with the interaction term is better, but this is not necessarily the case because the predicted value of the upper right area is not 1.

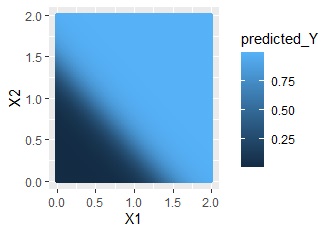
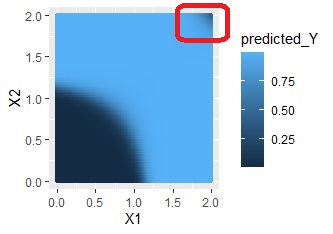
This is the case for distributions like XOR conditions. Without interaction terms, it is completely useless, but with interactions, we can predict with great accuracy.
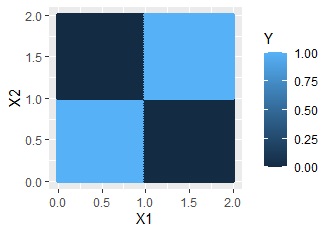

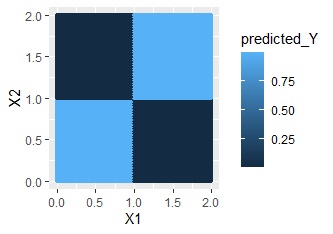
In a Linear Mixed Model, you create an interaction term for variables with only ones and zeros and quantitative variables. This allows you to create a regression model that fits only 1 sample.
This alone is no different from the story of only 1 sample, but in the linear mixed model, we will create a complex model by multiple regression analysis of multiple interaction terms created in this way.
An application of linear mixture models is Interval High-dimensional regression analysis.
