pca_dataB <- transform(pca_data2 ,name1=rownames(pca_data2),name2="B")# 言葉の散布図
library(ggplot2)
library(plotly)
ggplotly(ggplot(pca_dataB, aes(x=PC1, y=PC2,label=name1)) + geom_text())# 言葉の散布図
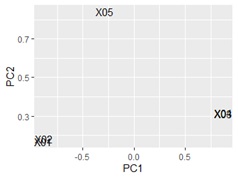
重なってわかりにくいですが、X01とX02が近く、X03とX04が近いです。
Rによる主成分分析の基本 にある変数の類似度の主成分分析の続きです。
Rによる主成分分析の基本 のコードと、以下は同じです。
setwd("C:/Rtest")
Data <- read.csv("Data.csv", header=T)
DataName <- Data$Name # Nameの列を別名で保管する
Data$Name <- NULL # データからNameの列を消して、Xの列だけにする
pca_model <- prcomp(Data, scale=TRUE) # 主成分分析
summary(pca_model) # 「Cumulative Proportion」が累積寄与率。
pca_data1 <- as.data.frame(pca_model$x) # 主成分得点を得る
pca_dataA <- transform(pca_data1 ,name1 = DataName,name2 = "A")# サンプル名を追加
pca_data2 <- sweep(pca_model$rotation, MARGIN=2, pca_model$sdev, FUN="*") # 因子負荷量を計算
pca_dataB <- transform(pca_data2 ,name1=rownames(pca_data2),name2="B")# 言葉の散布図
library(ggplot2)
library(plotly)
ggplotly(ggplot(pca_dataB, aes(x=PC1, y=PC2,label=name1)) + geom_text())# 言葉の散布図

重なってわかりにくいですが、X01とX02が近く、X03とX04が近いです。
基本の分析だと、2つの主成分を散布図の縦軸と横軸にして考察します。
2つの主成分のすべての組合せを見る方法がありますが、「結局、どの変数同士が近いのか?」ということが、考察しにくいです。 そこで、 高次元を2次元に圧縮して可視化 の方法で、多次元を2次元にします。
なお、この例だと、基本の分析の時と特に変わらない結果になります。 意味のある主成分の数が、もっと増えると効果的な方法になります。
主成分との関係の情報は不要で、変数の類似度だけを詳しく調べたい場合は、 多次元尺度構成法 を使って、 多数の主成分を2つに凝縮すると良いです。
library(MASS)# ライブラリを読み込み
Data11_dist <- dist(pca_data2)# 主成分間の距離を計算
sn <- sammon(Data11_dist) # 多次元尺度構成法
output <- sn$points# 得られた2次元データの抽出
Data2 <- cbind(output, pca_dataB) # 元データと多次元尺度構成法の結果を合わせる。
ggplotly(ggplot(Data2, aes(x=Data2[,1], y=Data2[,2],label=name1)) + geom_text()) # 言葉の散布図
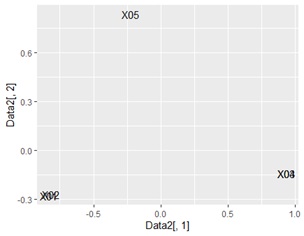
X01とX02、X03とX04の組合せがあることがわかります。
高次元データのネットワーク分析 を使う場合です。
library(MASS)# ライブラリを読み込み
Data11_dist <- as.matrix(dist(pca_data2))# 主成分間の距離を計算
library(igraph) # パッケージを読み込み
diag(Data11_dist) <- 1 # 対角成分は1にする
Data11_dist2 <- 1/Data11_dist # 近いほど小さい尺度に変換
diag(Data11_dist2) <- 0 # 対角成分は0にする
Data11_dist3 <- Data11_dist2 / max(Data11_dist2) *10 # 最大値が10になるように変換
Data11_dist3[Data11_dist3 < 1] <- 0 # 1より小さい場合は0に変換
DM.g<-graph.adjacency(Data11_dist3,weighted=T, mode = "undirected") # グラフ用のデータを作る
plot(DM.g, edge.width=E(DM.g)$weight) # グラフを作る
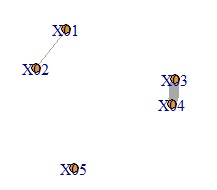
X01とX02、X03とX04の組合せがあることがわかります。
基本の分析だと、2つの主成分を散布図の縦軸と横軸にして考察します。
主成分得点(相関係数)は、2乗すると寄与率になる性質を使います。
library(MASS)# ライブラリを読み込み
pca_data22 <- pca_data2^2 # 寄与率(相関係数の2乗)を計算
pca_data22[pca_data22 < 0.5] <- 0 # 寄与率が以下の関係は見ないことにする
pca_data22

この結果を見ると、
(PC1と、X01、X02、X03、X04)、(PC2と、X05)で、それぞれ相関が高いことがわかります。
主成分と元の変数の相関の強さの全体像を見るためのグラフを作ってみます。
library(igraph) # パッケージを読み込み
pc4<-pca_data22*2 # 線の太さを変更
DM.g<-graph_from_incidence_matrix(pc4,weighted=T) # グラフ用のデータを作る
V(DM.g)$color <- c("steel blue", "orange")[V(DM.g)$type+1] # 色を変える
V(DM.g)$shape <- c("square", "circle")[V(DM.g)$type+1] # マークの形を変える
plot(DM.g, edge.width=E(DM.g)$weight) # グラフを作る

表のデータが、グラフで見やすくなりました。
主成分得点(相関係数)は正負があるため、それを分けてグラフにする方法も考えられます。
なお、この方法は筆者が思い付いて作ってみたものですが、実務で役に立った経験は、今のところないです。
library(igraph) # パッケージを読み込み
library(sigmoid) # パッケージを読み込み
Data1p = pca_data2# 分析対象のデータを抽出
colnames(Data1p) = paste(colnames(Data1p),"+",sep="")# 列名を変更
DM.matp = apply(Data1p,c(1,2),relu)# 0以下の値は0に変換
Data1m = -pca_data2# 分析対象のデータを抽出。符号を反転
colnames(Data1m) = paste(colnames(Data1m),"-",sep="")# 列名を変更
DM.matm = apply(Data1m,c(1,2),relu)# 0以下の値は0に変換
DM.mat =cbind(DM.matp,DM.matm)# プラス側とマイナス側を合体
DM.mat <- DM.mat / max(DM.mat) * 3 # 値が0から3になるように変換(線の太さになる)
DM.mat[DM.mat < 1] <- 0 # 1未満の場合は0にする(非表示にする)
DM.g<-graph_from_incidence_matrix(DM.mat,weighted=T) # グラフ用のデータを作る
V(DM.g)$color <- c("steel blue", "orange")[V(DM.g)$type+1] # 色を変える
V(DM.g)$shape <- c("square", "circle")[V(DM.g)$type+1] # マークの形を変える
plot(DM.g, edge.width=E(DM.g)$weight) # グラフを作る

因子負荷量は、プラスとマイナスがあり、絶対値が大きいほど、元の変数と相関が高いことを表します。 例えば、PC1という因子負荷量については、元の変数には、プラス側で相関が高い場合、マイナス側で相関が高い場合、相関が低い場合の3つに分かれます。 このことがわかるように、PC1という変数から、「PC1+」と「PC1-」という変数を作るようにして、どちらと相関が高いのかがわかるようにしてみました。
RStudioで、このページのコードを扱う時の注意です。
上のコードの場合、散布図は、「Viewer」の所に出ます。
ネットワークグラフは、「Plots」の所にできます。
「グラフができない」となった時の確認ポイントです。



