Rによるデータ分析

Rによる主成分分析の基本

主成分分析のRによる実施例です。

主成分分析の基本

主成分分析の使い道はいろいろですが、以下は順を追って説明しています。

モデルを作る

Rの実施例は下記になります。下記は、コピーペーストでそのまま使えます。

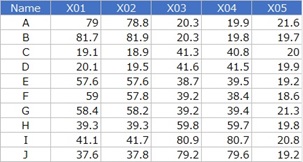
サンプルのデータは下記を使っています。「Name」の列はなくても動きます。
PCA

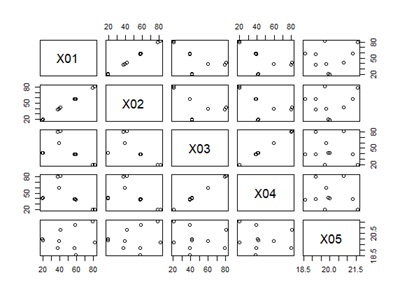
X01とX02、X03とX04の組合せはｍ相関が高いです。それ以外の組合せは相関がないです。
PCA

setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
DataName <- Data$Name # Nameの列を別名で保管する
Data$Name <- NULL # データからNameの列を消して、Xの列だけにする
pca_model <- prcomp(Data, scale=TRUE) # 主成分分析
summary(pca_model) # 「Cumulative Proportion」が累積寄与率。
PCA

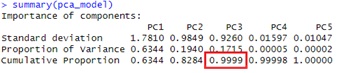
PC3までで、累積寄与率が0.999になっています。変数は５個ありますが、３個まで減らしても、情報量は特に変わらないことがわかります。

相関が高い組合せが２組あるので、主成分分析をしなくても、5 - 2 = 3という予想ができますが、その通りになりました。

「次元削減」のデータを作る

上記のコードの続きです。「他の多変量解析で、データの前処理に使う」をするために必要な主成分得点を得る方法です。

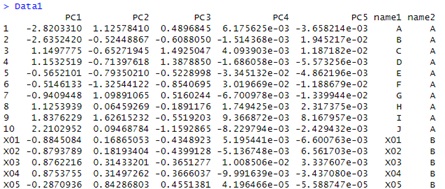
pca_data1 <- as.data.frame(pca_model$x) # 主成分得点を得る

作ったデータは下のようになっています。
PCA

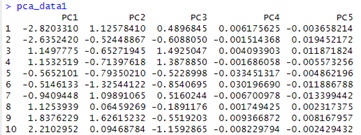
例えば、累積寄与率を見て２つ目の主成分までを使うことにするのなら、「pca_data1」の左の２列が次元削減後のデータということになります。

サンプルの類似度の分析の基本

上記のコードの続きです。「総合的にサンプルを見る」や「サンプルの仲間分け」の方法です。これを進めるには、ggplot2のインストールが事前に必要になります。

行番号でグラフを作ります。
library(ggplot2)# ライブラリを追加
library(plotly)
ggplotly(ggplot(pca_data1, aes(x=PC1, y=PC2,label=rownames(pca_data1))) + geom_text())# 第１主成分と第２主成分で言葉の散布図
PCA

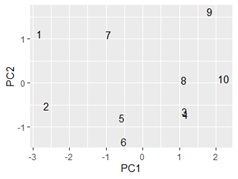
ggplotlyを使っているので、文字が重なっているところは、範囲を指定すれば、拡大して見れます。
PCA PCA

「Name」の列があるデータを使う場合、「Name」でグラフを作ることもできます。
pca_dataA <- transform(pca_data1 ,name1 = DataName,name2 = "A")# サンプル名を追加
ggplotly(ggplot(pca_dataA, aes(x=PC1, y=PC2,label=name1)) + geom_text())# 第１主成分と第２主成分で言葉の散布図
PCA

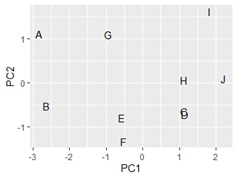
詳しくは、 Rによるサンプルの類似度の主成分分析

変数の類似度の分析の基本

pca_data2 <- sweep(pca_model$rotation, MARGIN=2, pca_model$sdev, FUN="*") # 因子負荷量を計算
pca_dataB <- transform(pca_data2 ,name1=rownames(pca_data2),name2="B")# 言葉の散布図
ggplotly(ggplot(pca_dataB, aes(x=PC1, y=PC2,label=name1)) + geom_text())# 言葉の散布図
PCA
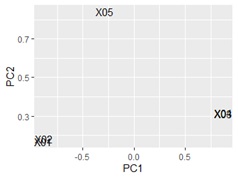
重なってわかりにくいですが、X01とX02が近く、X03とX04が近いです。

詳しくは、 Rによる変数の類似度の主成分分析

A-B型の分析の基本

biplotを使うと、サンプルと変数を同時に描いた図が作れます。
biplot(pca_model) # グラフを作る
PCA

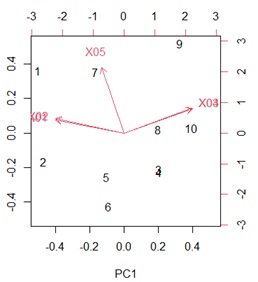
このグラフを作るためのデータは、下記で作れます。
Data1 <- rbind(pca_dataA,pca_dataB)# データを結合
PCA

詳しくは、 Rによるクロス集計表の主成分分析や Rによる質的変数の主成分分析

Rによるデータ分析