 Rによるデータ分析
Rによるデータ分析
 Rによるデータ分析
Rによるデータ分析
高次元を2次元に圧縮して可視化 のRによる実施例です。
MDS、t-SNE、UMAP、SOM、LLEに使うデータを作ります。
基本的に量的変数を扱いますが、質的変数はダミー変換するコードにしてあるので、 量的と質的変数が混ざっていたり、質的変数だけでもできます。
library(dummies) # ライブラリを読み込み
library(som) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data # 加工用のデータの作成
Data1$Name <- NULL # データからNameの列を消す
Data2 <- dummy_cols(Data1,remove_first_dummy = FALSE,remove_selected_columns = TRUE)# ダミー変換
Data3 <- normalize(Data2[,1:ncol(Data2)],byrow=F)# 標準化
グラフに使うデータを作ります。
MDS、t-SNE、UMAP、SOM、LLEは、一長一短なので、使い分けると良いようです。
・長所:ハイパーパラメタがないので、一番簡単
・短所:すべて質的変数だと、エラーになる。距離が0になるサンプルの組合せがあるとエラーになる。
library(MASS) # ライブラリを読み込み
Data4 <- dist(Data3)# サンプル間の距離を計算
sn <- sammon(Data4) # 多次元尺度構成法
Data5 <- sn$points# 得られた2次元データの抽出
・長所:想定通りのグループになりやすい。
・短所:パラメタの調整が必須。距離が0になるサンプルの組合せがあるとエラーになる。
perplexityが小さいと、プロットが重なりやすくなります。
perplexityはデフォルトが30になっていて、サンプルが少ない場合はエラーになりやすいです。
この実施例のデータでperplexityを何も設定しないとエラーになります。
ここでは、「perplexity = 3」にしています。
library(Rtsne) # ライブラリを読み込み
ts <- Rtsne(Data3, perplexity = 3) # t-SNE
Data5 <- ts$Y# 得られた2次元データの抽出
・長所:想定通りのグループになりやすい。距離が0になるサンプルの組合せがあってもエラーにならない。
・短所:どのグループにも属さないようなサンプルでも、どこかのグループに入れてしまう
n_neighborsが小さいと、プロットが重なりやすくなります。
n_neighborsはデフォルトが10のようで、サンプルが少ない場合はエラーになりやすいです。
ここでは、「n_neighbors = 5」にしています。
library(Rcpp) # ライブラリを読み込み
library(umap) # ライブラリを読み込み
ump_out <- umap(Data3,n_neighbors=5) # UMAP
Data5 <- ump_out$layout# 得られた2次元データの抽出
・長所:すべて質的変数でも、エラーにならない。
・短所:計算時間が長い。
格子を多くすると、計算時間も長くなる。
library(som) # ライブラリを読み込み
sm <- som(Data3,xdim=10,ydim=10) # 自己組織化マップ。10×10の格子に振り分ける場合
Data5 <- sm$visual# SOMによって、得られた2次元データの抽出
・長所:中程度の局所的な構造がわりとうまく出る。
・短所:kの調整が必要。kが大きいと計算時間が長い。
library(lle) # ライブラリを読み込み
le <- lle(Data1, m = 2, k = 20) # LLEの実施 # LLE。mが削減後の次元数。kがクラスターの数で、わからない時は大きめが良い。
Data5 <- le$Y# LLEによって、得られた2次元データの抽出
library(ggplot2) # ライブラリを読み込み#
Data6 <- cbind(Data5 ,Data) # 2次元に凝縮されたデータに、元データを合体
ggplot(Data6, aes(x=Data6[,1], y=Data6[,2],label=Name)) + geom_text() # Nameを使った言葉の散布図
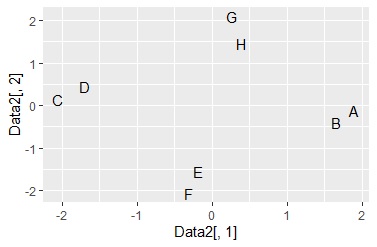
近くに配置されているほど、類似していることを表します。
縦軸と横軸の数値には定量的な意味はありません。
自己組織化マップでは、同じ格子に分類されると、同じ座標になるため、グラフ上で重なります。
重なりを解くために、少しばらつかせるのなら、下記にすると良いです。
「0.2」としているところを変えると、ばらつき方が変わります。
あまり大きくすると、隣の格子と区別がつかなくなります。
ggplot(Data6, aes(x=Data6[,1], y=Data6[,2],label=Name)) + geom_text(position=position_jitter(0.2))
library(ggplot2) # ライブラリを読み込み#
Data6 <- transform(Data5 ,Data,Index = row.names(Data)) # 2次元に凝縮されたデータ、元データ、元データの行番号を合体
ggplot(Data6, aes(x=Data6[,1], y=Data6[,2],label=Index)) + geom_text() # 行番号を使った言葉の散布図
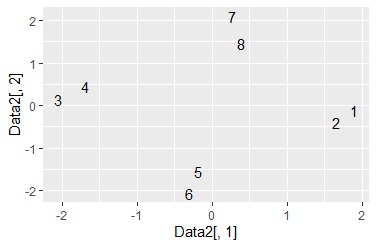
library(ggplot2) # ライブラリを読み込み
Data6 <- transform(Data5 ,Data, Index = row.names(Data)) # 2次元に凝縮されたデータ、元データ、元データの行番号を合体
Data6$Index <- as.numeric(Data6$Index) # Indexを数値型に変換
ggplot(Data6, aes(x=Data6[,1], y=Data6[,2])) + geom_point(aes(colour=Index)) + scale_color_viridis_c(option = "D")# 行番号を使った散布図
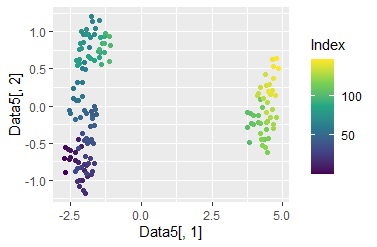
サンプル番号で色分けされています。
グラフの作成3の例では、データが大きく2つの領域に分かれることがわかりました。 そこで、この2つに色を付けます。
思ったような色分けになるとは限らないのですが、クラスター分析を使うと、グループ分けした変数を簡単に作ることができます。
library(ggplot2) # ライブラリを読み込み
library(mclust) # ライブラリを読み込み
mc <- Mclust(Data6[,1:2],2) # 混合分布によるクラスター分析。これは2個のグループ分けの場合
Data7 <- transform(Data6 ,clust = mc$classification) # クラスター分析の結果とデータを合体
Data7$clust <- as.factor(Data7$clust) # clustを文字型に変換
ggplot(Data7, aes(x=Data6[,1], y=Data6[,2])) + geom_point(aes(colour=clust)) # グループごとに色分けした散布図
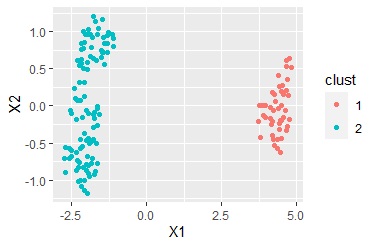
サンプルの類似度の分析では、サンプルがいくつかのグループに分かれることがありますが、何によって分かれたのかがわかりません。
この後の分析としては、
カテゴリの類似度の分析
で
Data <- read.csv("Data.csv", header=T)
の部分を
Data <- Data7
に変更して、clustの内容と他の変数の関係を調べる方法があります。
上記で、多次元尺度構成法は、コードの中に距離行列を作る部分があります。 そのため、距離行列の形のデータを最初に持っている場合のやり方は、想像しやすいです。
t-SNE、UMAPも、距離行列による次元圧縮 の方法です。距離行列の形のデータから分析をスタートすることはできます。
また、アウトプットの次元数を2次元以外にすることもできます。 下記の例では、3次元にしています。
library(MASS)
sn <- sammon(DM, k = 3)
Data5 <- sn$points
library(Rtsne)
ts <- Rtsne(DM, perplexity = 3, dims = 3)
Data5 <- ts$Y
t-SNEの場合は、dimを4以上にすると、エラーになります。
library(Rcpp)
library(umap)
ump_out <- umap(DM,n_neighbors=5, n_components = 3)
Data5 <- ump_out$layout

