平均処置効果と個別処置効果の関係

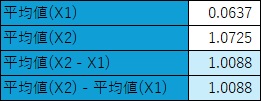
causal_effect
上の表は、サンプル数が100個のデータの集計結果です。 X1とX2という2つの変数があります。 X1とX2は独立しています。

この表から、X2とX1の差を計算してから、その平均値を計算した場合と、X1とX2について、個別に平均値を計算してから差を計算した場合で、同じになることがわかります。つまり、個別処置効果が計算できなくても、平均処置効果は計算できます。

分散の場合

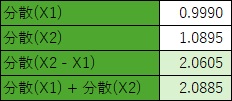
causal_effect
分散については、X2とX1の差を計算してから、その分散を計算した場合と、X1とX2について、個別に分散を計算してから和を計算した場合で、ほぼ同じになります。

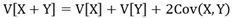
causal_effect
Vが分散で、Covが共分散です。２つの変数が独立していると、理論上は、共分散は０になりますが、実際のデータでは、正確に０にはならず、ほぼ０になります。そのため、「ほぼ同じ」という計算結果になります。

対応のないデータでは、個別のサンプルについて、「X2 - X1」が計算できません。

しかし、上記の平均値と分散の性質を使うと、「X2 - X1」が計算できないデータだとしても、「X2 - X1」という変数の、平均値と分散を近似的に求めることができます。

この計算は、平均値の差の検定のo値A で使います。