ゼロ十分数

伝統的な統計学にあるサンプル数の決め方は、３つの観点に分けられるようです。

このページのタイトルにした「ゼロ十分数」というのは、筆者の造語です。「信頼区間をゼロにするのに十分なサンプル数」というところから付けました。

「多過ぎるサンプル数は、ムダ」という考え方をしています。

伝統的な統計学と、サンプル数の考え方

ひとつのサンプルの測定に、お金、時間、手間がかかる場合、サンプル数は、できるだけ少なくしたいです。

一方、ある程度の数は、準備しないと統計学的な検証ができないです。

サンプル数の決め方は、この観点でされることが多いです。

数理統計学では、伝統的に、推定値がどこまで真の値に近付けるのかが研究テーマになっています。一致性、不偏性、漸近性、といった性質が、数学的に研究されて来ました。

「サンプル数は、多ければ多いほど、真の値に近付く」ということは、素人でも推測できますが、それを数学的に厳密に探求してきた歴史があるようです。

「P値は、サンプル数に依存する量になっていて、研究で不便」という問題への対策として、サンプル数を固定する統計学があります。「サンプル数は、いくつ以上取るべきか？」の統計学のセットにして使います。

「サンプル数は、多ければ多いほど良い」には反するのですが、このような手法もあります。

なお、「P値は、サンプル数に依存する量になっていて、研究で不便」という問題の根本的な問題は、研究に合わない統計手法を採用してしまったことにあります。そのため、「サンプル数は、多ければ多いほど良い」を否定するものではないです。

統計手法が合っていないのですが、その統計手法を使いたいため、苦肉の策として、サンプル数の上限を決める形になっています。

統計学を数理的に探求すると、「サンプル数は、多ければ多いほど良い」となるのは、これはこれで正しいと思います。

例えば、数理統計学では、サンプル数が無限大になれば、信頼区間は無限小になります。これを「ゼロになる」とみなすことはできます。

ところで、数理統計学は、純粋に数学の話になっていて、有効数字と分解能の観点がありません。有効数字と分解能を考慮すると、無限大よりも小さなサンプル数でも、「信頼区間がゼロ」になります。

そのサンプル数よりも多過ぎる分は、分析でムダになります。

信頼区間に最小値がある統計学の場合、「多過ぎるサンプル数は、ムダ」となります。

従来の数理統計学から出て来るのは、「サンプル数は、多ければ多いほど良い」という結論です。

一方、有効数字や分解能を考慮すると、「サンプル数が多い」には、信頼区間がゼロになる場合と、ならない場合に分かれます。これは、「サンプル数が無限大になるか、ならないか」、とは異なります。

話は変わりますが、物理学では、原子の大きさが、ひとつの区切りになっています。日常生活では、原子の大きさよりも大きいものだけを気にしていれば何の問題もないです。しかし、原子の大きさよりも、小さな世界の物理学が探求されることで、宇宙の研究に役立ったりしています。

計測学・数理統計学・数理物理学が合わさったような学問にも、意義があるのかもしれません。

下のグラフは、平均値０、標準偏差１の場合の信頼区間の上側（Upper）です。横軸が、サンプル数（N）です。

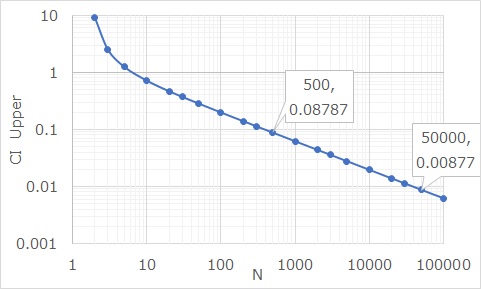
有効数字や分解能に対して、どこまで測れていると考えるのかは、いくつか考え方が分かれるかもしれませんが、例えば、「有効数字が0.1の時は、0.1未満の数字は0」と考えるのなら、Nが約500の時に、0.1未満になっている事がグラフから読み取れます。 Nが約50000の時に、0.01未満です。

この「500」や「50000」が、ゼロ十分数です。

ざっくりとした筆者の感覚ですが、標準偏差が１くらいの物を測るのに、工場で使う測定器は、0.1くらいの精度で管理することが多いです。そのため、「500くらいあれば良く、それ以上はムダになってしまう」と考えることができます。

上の例と同じですが、信頼区間がゼロになることから考えるのなら、下記の式になります。 sが標準偏差です。

標準誤差がゼロになることから考えるのなら、下記の式になります。