粗い測定の相関性

相関係数を使った研究は、分野を問わずあります。

心理学など、データがアンケート調査によるものだった場合、順序尺度のデータです。順序尺度でなかったしても、精度の粗い測定値の場合もあります。

このようなデータの場合、相関係数に含まれるデータのばらつきには、測定の粗さによるものが含まれます。以下では、測定の粗さの影響を調べたものです。

結論を先に書くと、例えば、３分割の粗さの場合（順序尺度で、１、２、３など）、相関係数Rは0.4以上、決定係数R2は0.2が、相関があるかどうかの目安になりそうです。これらよりも小さい場合は、２つの変数間に何かの関係があるかは、考えにくくなります。

粗さの影響の分析方法

例えば、精度が細かく測定できたすれば、左のグラフのようになるのに、粗いために、右のグラフのようになっていると考えられる場合があります。

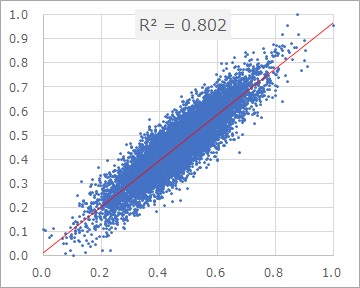
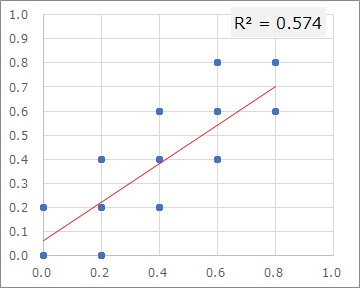
この例は、左のグラフのデータを作ってから、５倍して小数点以下を切り捨ててから、５で割ることで、粗いデータに変換することで、右のグラフのデータを作っています。サンプル数は1000です。

この例の場合は、約23%が測定の粗さの影響と考えられます。

上の例では、細かいデータの時に、R2が0.802の時に、５分割したデータになった場合です。

この調べ方をさらに進めて、R2の数値と、分割の数をいろいろ変えて、調べた結果が下のグラフになります。横軸は、連続データで細かい（Smooth）な場合です。縦軸は、粗い(Rouph）な場合です。赤い丸で囲っているのが、上の例の場合になります。

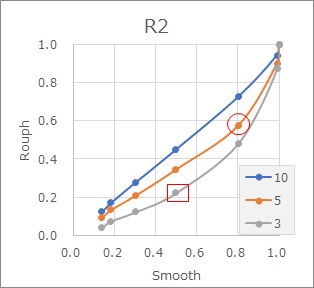
R2のグラフでは、横軸が0.3から0.8の領域について言えば、「10分割の時0.1、３分割の時0.2くらいR2が低くなる」となっています。

目安になるポイントは、赤い四角で囲っているのが、３分割で、細かい時にR2が約0,5になる場合です。 R2が0.5というのは、「約半分の寄与率で説明できる」ということで、因果関係がある可能性の目安になります。

３分割の場合、R2が0.2の時は、細かい時は0.5です。そのため、３分割の場合は、R2が0.2くらいあれば、「因果関係の可能性を考えても良さそう」という考察ができます。

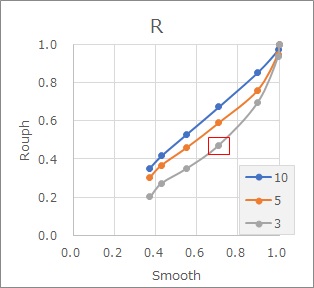
下のグラフは、相関係数Rとして計算したものです。

R2が0.5に相当するのは、Rでは0.7（0.7*0.7=0.49なので）です。３分割の場合、Rが0.4～0.5の時に、細かいデータでRが0.7になります。

相関係数の検定をして、例えばP値が0.0002だったということを根拠にして、「相関係数が0.1だが、P値が小さいから、これは意味のある相関関係がある」という考察をした場合、これは誤用になります。（この話は、相関の検定のページで詳しく説明しています。）

このページでは、連続データでは、「相関なし」と判断されるような相関係数が小さいケースでも、粗いデータの場合は、「相関がありそう」と判断した方が良いことを説明しています。ただし、どんなに小さな相関係数でも、「相関がありそう」とはならないので、粗いデータの時の目安を調べています。