トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

分散の比の検定でできないこと

ばらつきの違いの検定 の一番ポピュラーなのは、分散の比の検定（F検定）です。

「ばらつきの違いの評価では、分散の比の検定を使う」という説明がされることが一般的と思いますが、２つの観点で、うまく行かない結果になりがちです。

少ないサンプル数では、極端に違う場合しか判定できない

平均値の差の検定 では、サンプル数が５くらいでも、実用的な分析になるのですが、分散の比の検定は、その程度だと役に立たないです。

例えば、下のグラフの場合は、２つのグループがそれぞれサンプル数が5ずつです。 ばらつきがかなり違うように見えますが、p値は0.059です。 一般的な判定基準だと、「ばらつきに違いがあるとは言えない」となります。

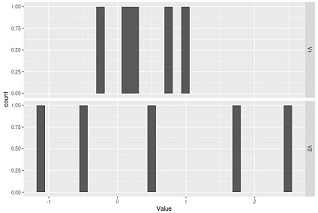
サンプル数が５の場合、標準偏差が８倍くらいは離れていないと、「違いがある」という検定にならないです。 また、上の図くらいの違いで「違いがある」という検定になるのは、サンプル数が50くらいは必要です。

こうなってしまう理由は、 誤差とn数 のページにあります。

サンプル数が多いと、「ばらつきの違いがない」という判定を出せなくなる

下のグラフの場合は、２つのグループがそれぞれサンプル数が10000ずつです。 ばらつきの違いはないように見えますが、p値は0.000000000000000000015です。 一般的な判定基準だと、「ばらつきに違いがある！！！」となります。

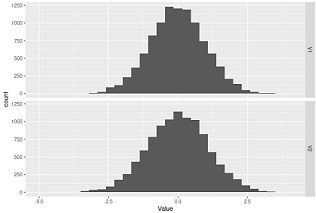
こうなってしまう理由は、 分散比とp値とサンプル数の関係 のページにあります。

順路 次は 分散比とp値とサンプル数の関係